1
信号简介
信号(singal)简介
我们在生活中经常遇到信号。比如说,股票的走势图,心跳的脉冲图等等。在通信领域,无论是的GPS、手机语音、收音机、互联网通信,我们发送和接收的都是信号。最近,深圳地铁通信系统疑似与WiFi信号冲突,也就是地铁的天线收到了WiFi的信号,而误把该信号当作地铁通信信号。我们的社会信息化,是建立在信号的基础上的。
信号是随着时间或者空间变化的序列。在信号处理中,我们常用“信号”来特指一维信号,也就是只随单一一个时间或空间维度变化的序列,这样的信号在数学上可以表示成f(t)或者f(x)这样一个函数。与一维信号形成对应的是多维信号,比如说图像是二维信号,它随x,y两个空间维度变化,从数学上表示成为f(x, y)。下面在没有特别声明的情况下,都使用“信号”来代指一维信号。
尽管信号的使用如此广泛,但信号从数学意义上来并没有什么神秘的地方,只是普通的序列(函数)。信号处理的方法可以通用于任何一个领域的信号(无论是通信、金融还是其他领域),这也是信号处理的魅力所在。
2
简谐波
简谐波(simple harmonic)
正弦波(sine wave)和余弦波(cosine wave)统称为简谐波。简谐波是自然界最常见的波动。

正弦波
正弦波可以写成函数的形式:

可以看到,一个简谐波三个参数,振幅(A, amplitude)、频率(f,frequency)、相位(phi, phase)。这三个参数分别控制正弦波的不同特征。通过调整它们,我们可以得到不同的正弦波信号。

左上:原始 右上:2倍振幅
左下:2倍频率 右下:相位移动
可以看到,频率高,“山峰”越密集。振幅高,“山峰”越高。相位改变,“山峰”的位置左右移动。(朋友说我是“用音量控制音调”:唱歌本应该改变频率高低的时候,却在改变振幅的高低。)
余弦波(cosine wave)函数形式与正弦波类似,用cos表示。我们可以通过改变正弦波来从正弦波获得余弦波。
3
傅立叶变换
傅立叶变换 (Fourier Transform)
简谐波虽然简单,但对信号处理具有重要意义。傅立叶是一名工程师,他发现,任何信号实际上都可以通过简谐波相加近似得到。也就是傅立叶定理(Fourier inversion theorem):任何一个信号都可以由简谐波相加得到。因此,复杂的信号可以分解成为许多个简单的简谐波。一个信号由多个频率的简谐波相加得到。组成信号的某个简谐波,称为信号的一个分量(component)。
比如下图,显示了我们如何用简谐波的叠加来不断趋近蓝色的信号:
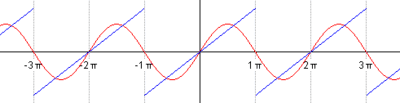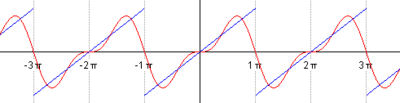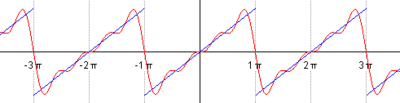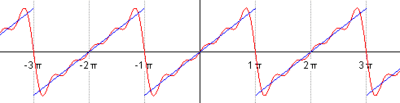
来自Wikipedia
傅立叶变换是一套固定的计算方法,用于算出信号的各个分量(也就是上面的an,bn)。在信号处理时,可以将信号进行傅立叶变换,转换为简谐波的组合。通过分别控制各个频率上的简谐波分量,我们可以更加有效的进行信号处理。比如说,我们通信的时候可以使用高频的简谐波信号。但是接收信号的天线可能会收到其他频率的干扰信号。这个时候,我们可以对接收到的混合信号做傅立叶变换,只提取目标高频的分量。这是降低信号噪音的常用方法。傅立叶变换的过程有些复杂,但已经有大量的程序可以帮你进行。你所需要的只是输入信号,计算机会帮你算出它的各个分量。
比如说,如果信号f(x)是周期性的,我们可以将它变换成:

也就是说,一个信号可以看做许多简谐波的和。上面的a,b是可以通过原信号求得的参数为:


a, b代表了信号在各个频率上的简谐波分量的强弱(以及相位)。这样,信号就分解为了简谐波的和。由于简谐波比较容易理解,我们可以通过研究这些分量,来明白复杂信号背后的机制。
4
频谱
频谱(frequency spectrum)
通过傅立叶变换,我们可以得到一个信号f(t)的不同频率的简谐波分量。每个分量的振幅,代表了该分量的强弱。将各个频率分量的强弱画出来,可以得到信号的频谱。比如下图是从每天降水序列中得到的频谱:

可以看到,以1年为周期的简谐波分量有一个明显的高峰。也就是说,一年周期的分量有比较强。这是有物理原因的。因为降水总是以一年四季为周期有规律的变化。通过信号-》Fourier Transform-》频谱,我们可以从简谐波分量的角度,理解复杂信号是由哪些简谐机制合成的。
图像处理(Image Processing)
傅立叶变换同样可用于多维信号。把傅立叶变换用于二维信号,即图像:

左边是二维信号(图像,f(x,y))。黑白可以用数值表示,即信号值。右边是二维图像的频谱。X轴表示x方向的频率,Y轴表示y方向的频率,黑白表示不同频率分量的振幅强弱。在下面一行中,Lenna被故意加上了噪声,并引起频谱的相应变化。频谱的中心代表了低频信号的振幅,频谱远离中心的地方代表了高频信号的振幅。 我们下面和加入噪声的图像比较。
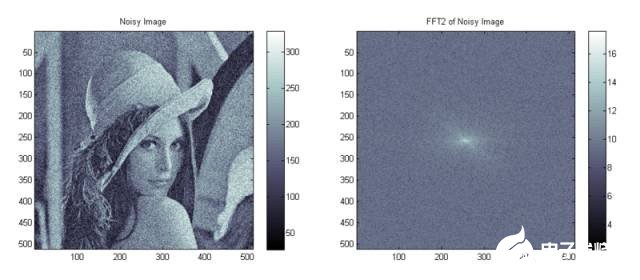
Lenna和她的频谱
现在,在图像中加入噪声。可以看到,原图像中各处增加了许多小“斑点”。这些斑点和原来的信号混合在一起。我们很难将一一指出这些噪音点。但另一方面,这些噪音又有一定的特征:这些噪音的空间尺度(即尺寸)很小。
这一对图像噪音的理解,可以从频谱中得到确认。从右图的频谱中可以看到,高频信号(非中心部分)明显增强。高频分量正对应空间尺度小的信号。可见,噪声在频谱中,集中在高频这一特定区域。这样,在与原图像混合在一起的噪声,在频谱上则和图像区分开。通过高频滤波技术,就可以过滤掉噪声。这也是图像降噪的一大方法。
(如果对图像处理有所了解,那么一定会知道Lenna的大名。她是一位阁楼(Playboy)女郎,但又是图像处理界的女神。你可以搜索“Lenna full image”来找到全图。Lenna现在是一名老太太了,她“见证”了图像处理的发展。)
5
总结
信号可以分解为不同频率的简谐波分量。这有助于我们更好的理解复杂的信号。傅立叶变换是信号处理(以及图像处理)的基础工具。通过傅里叶变换,我们可以获得信号的频谱。
频谱为我们提供了理解信号的另一个视角。在频率的世界里,我们可以发现很多原信号中一些可能被忽视的信息,比如降水的季节变化,比如增强的噪声。
2. 日本5G频段汇总
日本5G频段主要包括3.7GHz、4.5GHz和28GHz频段,其中3.7GHz&4.5GHz分配100MHz带宽,28GHz 分配400MHz带宽。
具体如下:

NTT DoCoMo:3600MHz-3700MHz、4500MHz-4600MHz和27.4GHz-27.8GHz频段
KDDI/冲绳移动电话:3700MHz-3800MHz、4000MHz-4100MHz和27.8GHz-28.2GHz频段
软银:3900MHz-4000MHz和29.1GHz-29.5GHz频段
乐天移动:3800MHz-3900MHz和27.0GHz-27.4GHz频段
责任编辑:haq
-
转换器
+关注
关注
27文章
9146浏览量
152585 -
信号
+关注
关注
11文章
2859浏览量
78587 -
频段
+关注
关注
1文章
335浏览量
24962 -
5G
+关注
关注
1360文章
48850浏览量
576684
发布评论请先 登录
信号噪声与远场频谱
是德频谱分析仪对微波信号频率稳定性的测量与分析
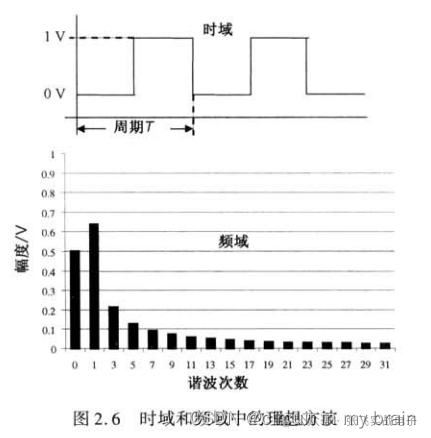
方波信号的频谱与带宽
是德频谱分析仪电子信号分析
是德频谱分析仪雷达信号测量
如何使用频谱分析仪进行信号测量
频谱分析仪与信号分析仪的区别
频谱分析仪的工作原理 频谱分析仪的应用领域
德国原装罗德与施瓦茨FSV3007信号/频谱分析仪
4052系列信号/频谱分析仪概述
Keysight 频谱分析仪(信号分析仪)






 科普:信号与频谱知识!
科普:信号与频谱知识!












评论