在树莓派Pico上运用不同的并行化手段

以下文章来源于嵌入式系统专家之声，作者Martin Ossmann

Martin Ossmann博士（德国）

翻译：何灵渊

树莓派Pico由RP2040微控制器驱动，其上搭载两个CPU核，这让它非常适合探索并行计算。本文通过真实的数字信号处理样例来说明从双核架构中提取最大价值的方法和考量。

本文中的样例运用了不同的并行化手段。通过双核处理器来加速一个程序的理论上限值为2，我们简称为S = 2。在下面的讨论中，我们会给出每一个样例的加速系数。

同步和“易变”属性

在多核CPU上编程时，时常需要让线程同步它们的活动。在下面这个最简单的例子中，核0可以激活核1，通过变量trigger就可以实现。

图1

两个核都会使用变量trigger，为了让编译器知道变量的值由于多个线程都可使用，随时可以改变，添加了“易变”（volatile）属性。没有这个属性，编译器可能会进行深入的代码优化，这也许会对两个线程的共享、并行使用造成不良影响。

共享函数的使用

下面的例子演示了核0和核1可以同时使用一个函数。

图2

函数delay(nn, cnt)中会打印消息列出正在运行的核和cnt的值，然后会进入等待循环执行nn次（使用本地变量k）。

核0和核1一样运行无限循环。循环内会调用delay函数，核0和1的nn参数分别为10000000和20000000，因此核1在delay函数中会执行双倍于核0次数的循环。cnt变量会跟踪循环执行的次数。两个核多数时间都会同时在delay函数中。函数的共享是如何做到的呢？函数的代码只会在内存中储存一份，两个核会执行同样的代码。代码中只有读指令，所以只是访问代码并不会造成冲突。

两个核当然有自己的程序计数器（PC），其中记载代码指令的地址（代码进行到了第几步）。当函数被调用时，PC的值会入栈，参数也会入栈，然后会在栈上预约空间存储本地变量（这里是k）。这一系列存储在栈中的变量也被叫做栈帧。PC接下来会载入被调用函数的起始地址。

两个核有独立的栈和栈帧，所以即使代码是共享的，两个核也各自有一个delay函数的“实例”，代码相同但是栈帧不同。如果delay函数中使用全局变量或者其他全局资源，分割就不复存在了，并行使用会导致问题。本例说明了并行编程需要考虑的问题。

核0可以影响核1的速度

下一个例子中我们将演示两个核如何会以不明显的方式互相影响。

图3

核1运行简单的无限循环，核0同样运行无限循环，但是会将GPIO2设为高电平，等待625个周期，将GPIO2设为低电平，然后再等待625个周期。当核1不运行时，以Pico默认时钟频率125MHz运行的核0每秒会运行10万次循环（125MHz/（2*625周期）），这会在GPIO2上输出一个100kHz频率的矩形波。当核1开始执行时，核0的这一输出信号频率会降到75kHz。尽管两个核之间没有明显的关联，它们还是会互相影响。这其中的可能原因是两个核共用同一个内存接口，这一现象通常可以解释为什么本文中程序的加速系数S一般都明显低于2。

本例突出了并行程序中存在的意想不到的效果，调试这样的并行程序可能会很有挑战性。

先入先出（FIFO）通信

你可以通过两个FIFO在两个核之间安全地传输数据，一个从核0向核1发送数据，另一个从核1向核0发送数据。Pico SDK中的FIFO是线程安全的，意味着即使并行使用也能正常运行。

为了测试FIFO的性能，我们可以在核1上实现一个简单的“服务器”：

图4

这段代码等待核0从FIFO发送数据，将得到的数字增加1000后返回给核0。

核0上运行的代码如下：

图5

运行时测量的数据表明，这段代码大概需要0.62微秒。因为每次传输的数据为32位，这等同于104Mbit/s。下面这一计数循环用于比较树莓派Pico的计算速度和数据传输率：

图6

测量数据表明，每次循环需要大约56纳秒。如果我们让服务器运行N = 10次，计算时间大约560纳秒，通信时间620纳秒，通信的开销比例大于100%。因此，如果不想要通信开销影响整体性能，服务器需要大幅提高计算能力。在并行计算环境中编程时，最好不要过于关注程序中最小的细节。除了FIFO，SDK也提供了队列，帮助传输任意数据结构，提供更大的灵活性。另外，SDK提供多种线程同步机制，推荐细致学习SDK提供的功能。

软件定义无线电（SDR）的并行化

图7所示的是SDR前端的组成，在将输入信号和本机振荡器（LO）信号相乘后，你得到了I频道（同相）和Q频道（正交）。两个频道几乎是并行的，非常适合并行计算。核0处理I频道的数据，核1处理Q频道的数据。混合后的相加依然由中断例程处理。第一个并行的部分是巴特沃斯滤波器的实现，使用单精度浮点数。在图8中，你可以看到低通滤波器的时间特征。

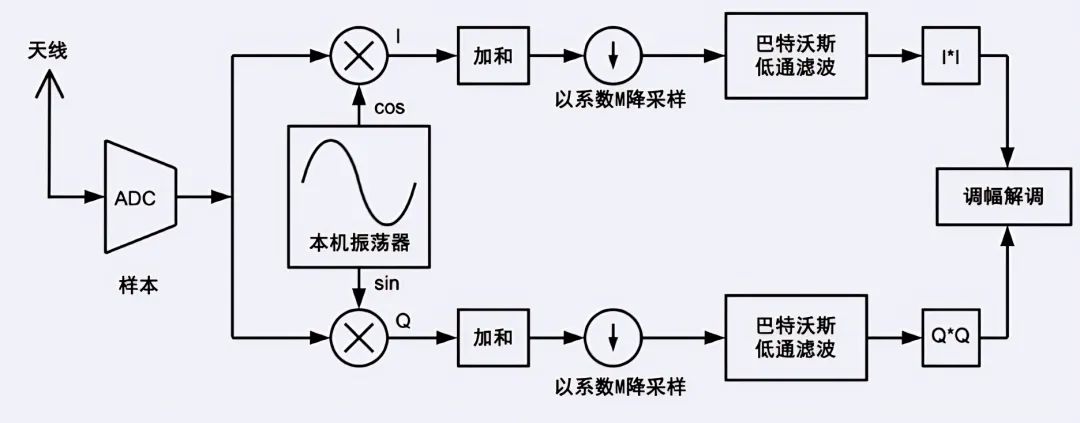
图7 SDR前端的信号流动

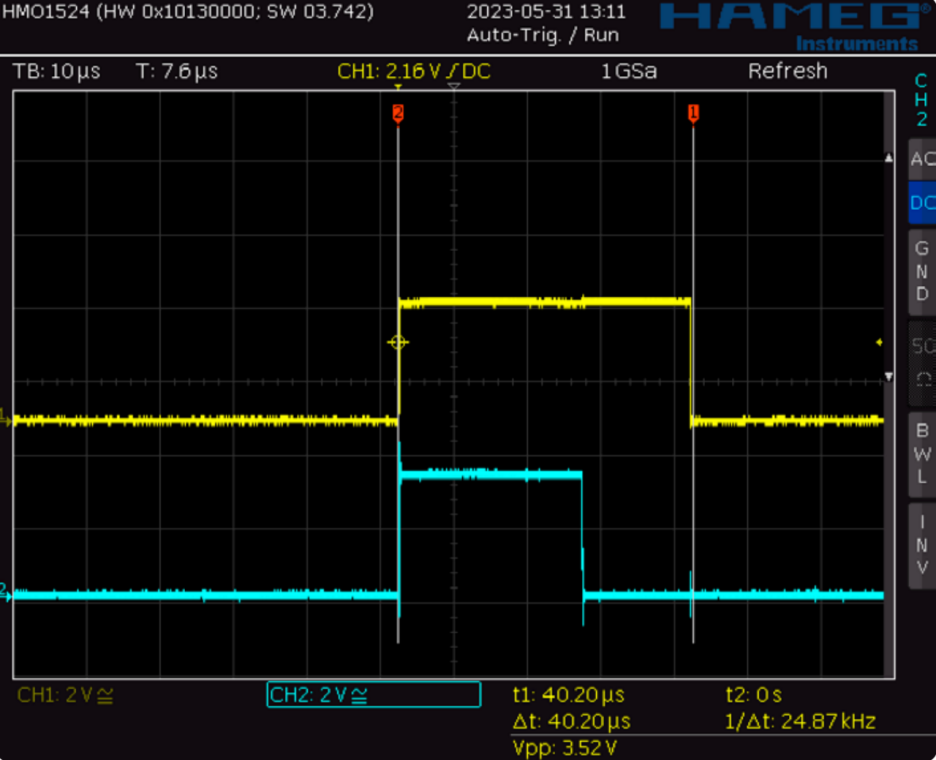
图8 I和Q低通滤波器例程的执行

核0进行I频道低通滤波器计算时会输出黄色的“高电平”，核1进行Q频道低通滤波器计算时会输出蓝绿色的“高电平”。有趣的是，I频道的计算需要更长时间，这是因为核0也执行中断例程进行取样，所以核0并不是一直可以使用，I频道的计算于是需要更长时间。

标量积和循环分割

另一个样例是标量积的计算。并行计算是基于以下的观察：通常一组计算以循环进行，如果一个循环中的元素可以单独计算，一个循环可以被分隔为两个部分，由两个核并行处理。计算两个向量x和y的标量积的公式如下图所示：

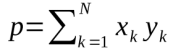
图9

程序中的skpLoop例程会通过下面的算式计算k1到k2的加和：

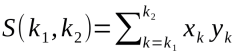
图10

在非并行的版本中，1到N的值会被直接加和。在并行的版本中，1到N/2和N/2到N的加和是并行进行的，算式如下图所示：

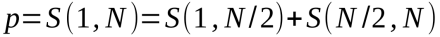
图11

最终结果通过两个部分相加得到。核0和核1同时使用skpLoop中的加和循环。因为循环由两个核分别使用，矩阵xk和yk各自不同，所以没有冲突。这一程序的加速系数S = 1.8，程序代码如图12所示。

图12串行和并行标量积计算

有限脉冲响应（FIR）滤波器

FIR滤波器在数字信号处理应用中有着广泛应用。在N阶的FIR滤波器中，当前输出值的计算需要将最后N个信号的值进行加和，期间会将样本和脉波响应系数ak相乘，公式如下图所示：

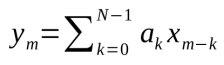
图13

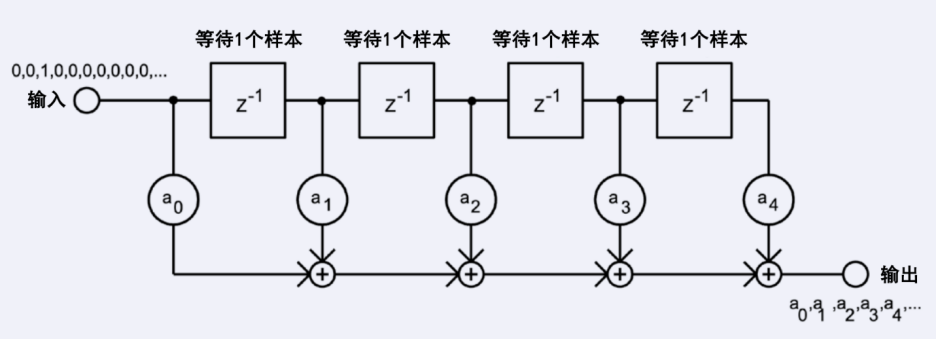
图14 FIR滤波器的信号流动

计算中需要将最后N个输入值xk存储起来，这可以通过一个环形缓冲区很容易地进行。计算的并行化和其他标量计算类似，可以通过循环分割来进行。你只需要正确地管理环形缓冲区和使用脚标。循环的逻辑如下图所示：

图15

readPtr参数指向环形缓冲区xBuf的起始位置。并行的FIR计算如下图所示：

图16

本程序的加速系数S = 1.7。

程序开发

调试并行程序经常既复杂又有挑战性。一般可以首先在一个更为灵活的环境中编写一个版本的程序作为参考版本，像是一个开源、免费的处理环境，然后在那里进行调试。在这一过程中，你可以生成用于并行的测试数据。这一版本的软件成型后可以移植到目标系统上，并用同样的测试数据进行测试。调试时你可以比较两个版本的软件行为。

带流水线的无限脉冲响应（IIR）滤波器

在数字信号处理中，IIR滤波器十分常用。IIR滤波器是一由系列双二阶单元（图17）组成的。非并行的形式中，一个单元的输入和上个单元的输出一致，也就是计算单元2前必需完成单元1的计算。

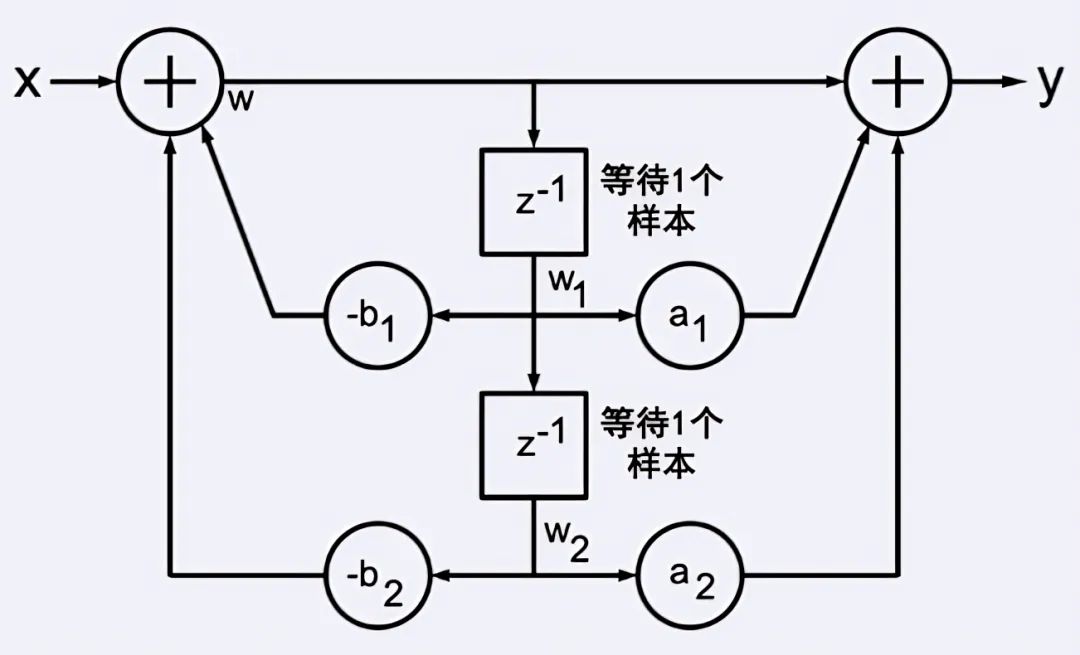
图17一个双二阶单元

每个单元取决于上一个单元的结果，用代码表示如下图所示：

图18

这使得双二阶单元计算的并行化变得困难，不过我们可以应用一种流水线技巧。流水线的概念是从实现快速的处理器开始的，将指令的执行分割为取指令、解码和执行三个步骤，不同命令的不同步骤可以同时执行。

当读取指令Ik时，上一个指令I(k-1)已经被解码，再上一个指令I(k-2)正在执行中（图19）。这样的并行处理能提高输出，单个指令并没有提速。

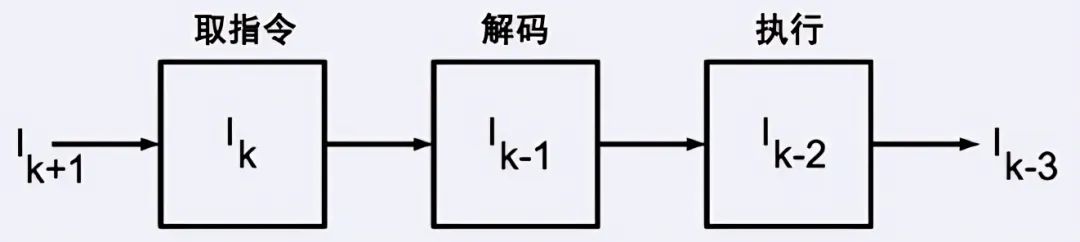
图19 CPU中的流水线

这一概念可以应用到IIR滤波器上，代码如下图所示：

图20

这里增加的中间值inp1到inp4让单元的计算互为独立，双二阶计算可以并行，这正是双核CPU上运行IIR滤波器的方法。这里的方法加速系数S大约为1.8。

就地执行（XIP）功能

如果你多次运行IIR滤波器并测量时间，你会有令人惊讶的发现（表1）。首次运行需要大约64微秒，这是后面运行的2.5倍左右。这一加速可以从RP2040访问代码存储的角度解释。代码在串行QPSI闪存中存储，CPU可以像直接访问CPU中数据一样访问（所以是就地执行，eXecute In Place——XIP）。由于闪存的访问使用串行接口，速度相对较慢。为了加速，XIP接口上有一个基于快速RAM的缓存，其中存储最近刚读取的内存字，所以同样位置的内存不需要经过QPSI接口，而是直接从缓存读取。

表1 IIR滤波器执行时间

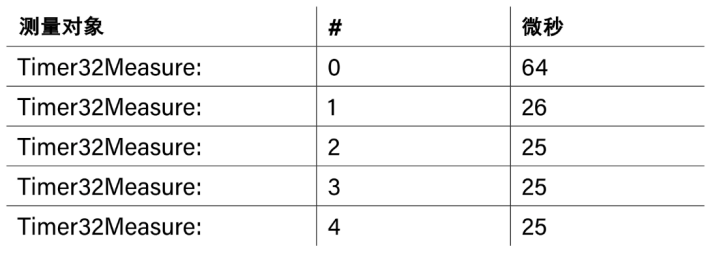
这一过程可以解释运行时间的数据。首次运行时，代码不能使用缓存，QSPI访问既慢又是串行性的。代码载入到缓存之后，再运行的速度就会变快。这从一方面说明现代CPU运行时行为的复杂性。你需要了解这样的机制，才能得到正确和可靠的结果。

快速傅里叶变换（FFT）

在数字信号处理中，快速傅里叶变换（FFT）时常用于分析信号。FFT计算由所谓的“蝴蝶操作”组成，蝴蝶操作中的数据流动如图21所示。

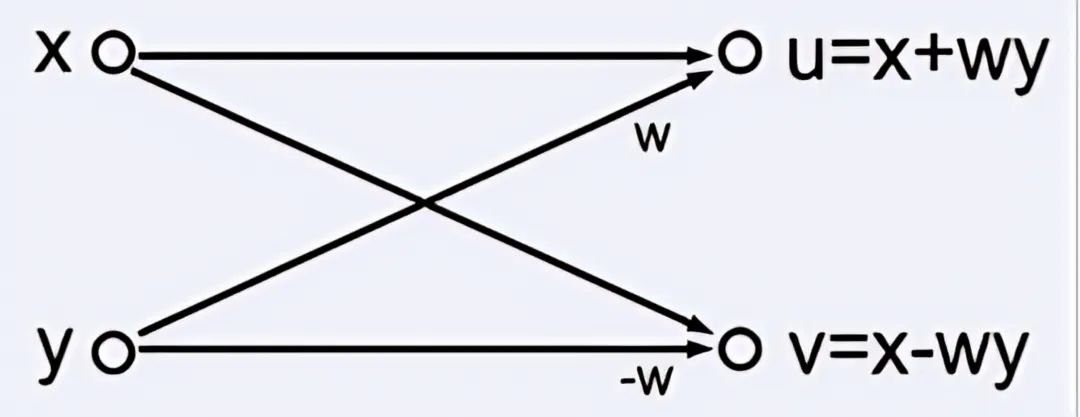
图21蝴蝶操作中的信号流动

图中系数w为与蝴蝶操作相关的相位的余弦。

图22表示N = 16时的数据流动，共进行log2N = 4次迭代，每次进行N/2个蝴蝶操作。在一次迭代中，蝴蝶操作互相独立，所以可以并行执行。一半的蝴蝶操作由核0执行，另一半由核1执行，每个核会执行N/4个蝴蝶操作。加速系数S = 1.85。

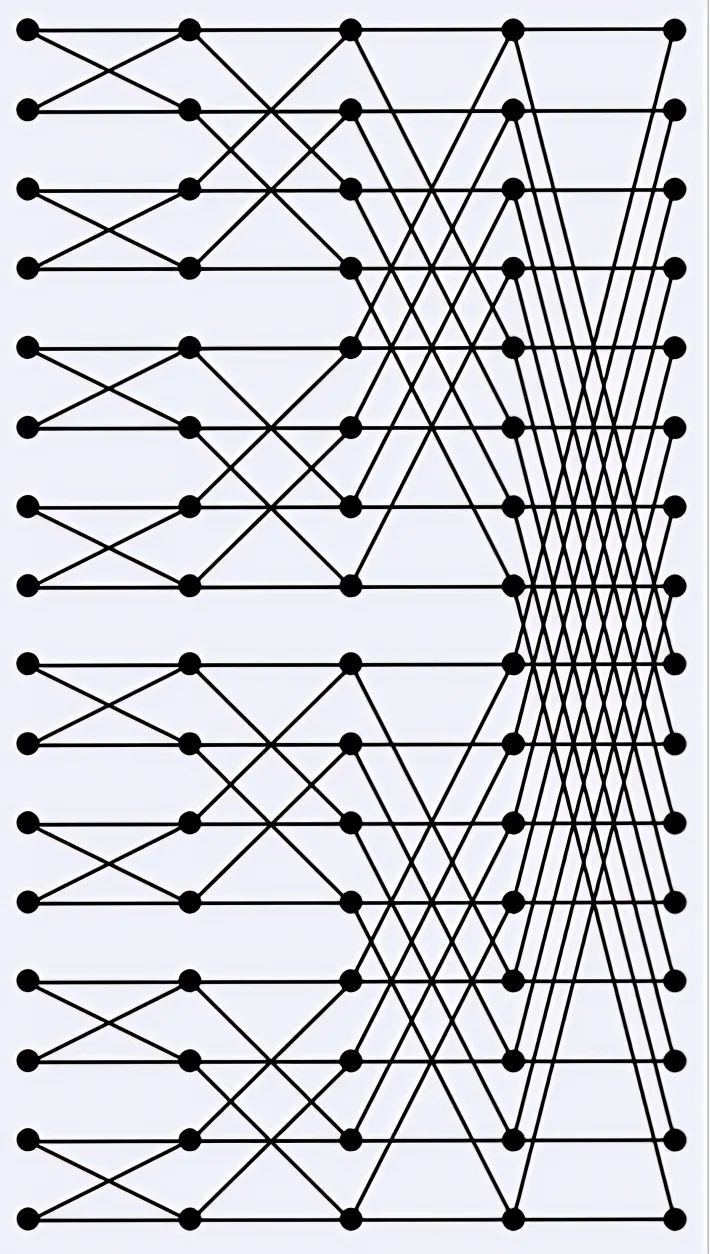
图22 16-点FFT的信号流动

霍纳法则

现在让我们把话题转向如何处理x阶的多项式。在下面的例子中，多项式为5阶，算式为：

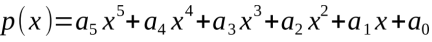
图23

求值需要N-1次乘法计算x的次方，N-1次与系数ak相乘，以及N次加法运算。霍纳法则给出了更加高效的计算方法。例如，可以通过下图中第一行的算式迭代计算5阶p(x)的值（译者注：p0为最终结果，第二和第三行通过展开多项式来证明p0和原多项式相等）：

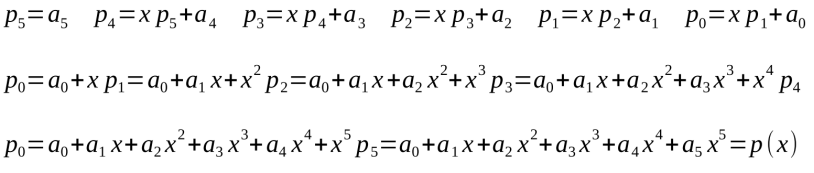
图24

最后，你会得到p(x)的值，而且只进行了N次乘法和N次加法，也就是说，总共节省了N-1次乘法。霍纳法则不能并行化，这是因为pk的值互相依赖，但是多项式本身可以被分割为两部分，如下图的算式所示：

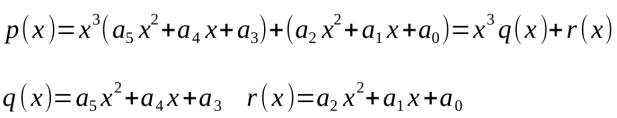
图25

现在我们可以同时求多项式q(x)和r(x)的值。要得到p(x)的值，只需要用x3（既x(N+1)/2）乘以q(x)加上r(x)。x(N+1)/2的快速计算非常重要，这可以通过利用连续乘方的结果1,x,x2,x4,x8,x16…来计算，例如x9= x8*x，计算需要log2N次。log2N相比N很小（特别是N很大时），计算会很快，不会特别影响性能。

N = 100时，在树莓派Pico上运行非并行版本需要133微秒，霍纳法则加上多项式分割的版本，两个核各自需要71微秒，将两者快速加和需要7微秒，也就是说并行算法需要78微秒，加速系数S = 133/78 = 1.7。x(N+1)/2的计算确实会影响效率，但是总体的提速效果依然很明显。

线性代数

除了点积，矩阵向量积也可以并行化，加速系数S = 1.6。线性方程组也可以并行化，S = 1.8。两个解决方案都使用了简单的循环分割方法。

真正的高效率

通过探索本文中的一系列实例，可以看到在双核的树莓派Pico上能够有效地将任务的执行过程并行化。实践中一些例子能达到S = 1.8，非常接近理论上限S = 2。最佳的并行策略需要合适的算法，寻找这样的算法的过程尤为重要。只有能够将任务分割，并独立、分别执行的方法，才能从并行处理中获得最大的效率提升。

关于作者

Martin Ossmann

Martin Ossmann在12岁时就开始阅读Elektor杂志和动手实验了。在学习电子工程，并作为工程师工作数年之后，他成为了德国亚琛应用科学大学电子工程和信息技术系的一名教授。他不仅是若干科学著作的作者，30年来他时常在Elektor杂志上发表新的电路或是软件项目，展示他丰富的专业知识。