实现SSC-EARSM湍流模型的关键技术

本文翻译转载于：Cadence Blog

作者：Gaurav

关键要点

●与简化基线显式代数雷诺应力模型（S-BSL-EARSM）相比，分离敏感型修正显式代数雷诺应力模型（SSC-EARSM）旨在更好地预测分离流动。

●SSC-EARSM 模型引入了三项关键改进：(1) EARSM 升级增强了对近壁各向异性的处理能力；(2) 剪切应力增强（SSE）可以提高剪切层中的湍流混合； (3) 尺度自适应模拟 (SAS) 可以进一步增强分离区域的混合能力。

实现 SSC-EARSM 湍流模型的关键技术

SSC-EARSM 是 Menter 等人 [2009] 提出的 S-BSL-EARSM 的改进版本。SSC-EARSM 引入了以下三项升级。第一项修正增强了各向异性的近壁表现，这与 EARSM 相关。另外两项修正，SSE 和 SAS，用于增强分离流和自由流之间剪切层中的湍流混合。

低雷诺数修正

Skote 等人 [2016] 提出了一种对 EARSM 模型的修正方法，以考虑低雷诺数效应，该方法类似 Van Driest 类型的阻尼函数。该函数仅在近壁区域起作用，其作用方式类似于涡粘性阻尼。与传统基于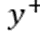?构建的阻尼函数不同，这种方法使用了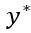，Skote 等人（2016）证明这种方法对分离流动更为适用。 该阻尼函数的定义如下：

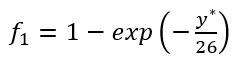
其中，

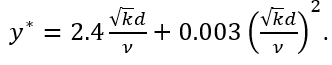
S-BSL_EARSM 的修改如下：

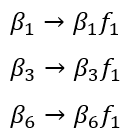
后验结果表明，涡粘性阻尼不足以获得平面流动的正确湍流能量峰值。虽然湍流能量的产生可以准确预测，但缓冲区（即湍流强度最大的区域）的耗散率过大，导致湍流能量过度耗散。因此，降低缓冲区的耗散率对于精确的湍流模拟至关重要。为此，使用 Abe 等人 [2003] 提出的阻尼函数来衰减 k 方程中的耗散率。该函数基于湍流和层流粘性之间的比率，仅在壁面附近有效。该阻尼函数如下：

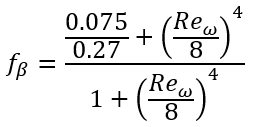
其中，

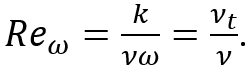
k 方程修改如下：

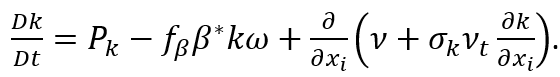
在非常靠近壁面的区域，耗散率并不准确。然而，由于该区域湍流较弱且粘性扩散占主导地位，这种不现实的耗散被平衡了，因此这一局限性对整体流动没有显著影响。

剪切应力增强

对 S-BSL-EARSM 的第二个修正是对湍流能量产生进行修改，以增强剪切层分离区域的剪切应力。在特定的流动区域，k 方程中的湍流能量产生会增加，并进行如下修正：

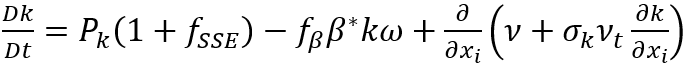
其中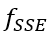是 SSE 函数。

当流体发生分离时，流向速度会出现一个拐点。从数学上讲，这个拐点被定义为流向速度的二阶导数为零的位置。因此，该点是流体最强剪切区域的位置，即分离的气泡剪切层。冯·卡门长度尺度是识别该增强区域的极佳方法。其定义为：

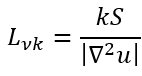
冯·卡门长度尺度在拐点附近趋于无穷大。因此，积分长度尺度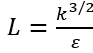?与冯·卡门长度尺度的比率在拐点附近的壁面附近趋于零。由此可以构建一个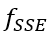，使得该函数在拐点附近具有统一的值，并在其他位置快速趋于零。为了避免校正影响近壁面区域，该函数与之前为低雷诺数校正定义的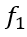?阻尼函数相乘。使用 Spalart [2006] 的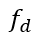函数在边界层中停用该函数，以便在计算附着边界层时最大限度地减少 S-BSL-EARSM 的影响。

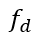函数用于混合模型，其中它在LES区域具有单一值，而在其他地方为零。经过进一步研究，其定义如下：

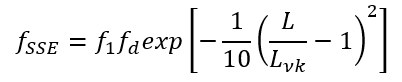
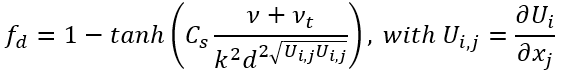
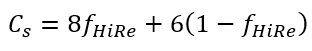
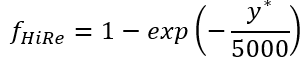
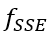函数中的 1/10 常数控制校正的程度。此外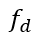，函数取决于局部雷诺数。对于较低的雷诺数，应增加校正量。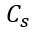函数中的系数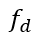也是局部雷诺数的函数。高和低局部雷诺数的常数值使用?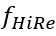?进行混合。请注意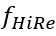，?是一个与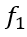?类似的阻尼函数，但阻尼程度更大。该常数的值是根据预测各种低和高雷诺数测试案例时获得的最佳折衷值得出的。

对分离校正项的敏感度

Maduta 等人 [2015] 提出的 SAS 项。它是对 Menter 的 SAS 公式在 Jakirlíc 和 Hanjalíc（2002）雷诺应力模型中的重新校准版本。其表达式为：

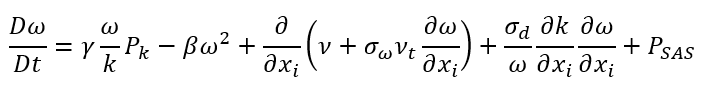
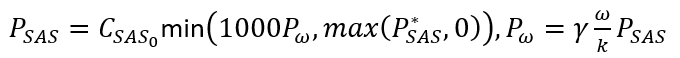
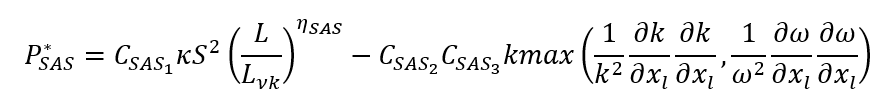
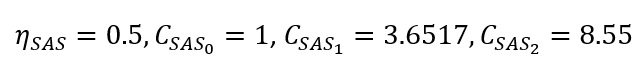
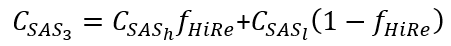
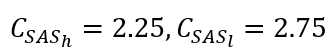
对于 SSE 项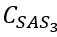，?的值是高雷诺数和低雷诺数的混合值。该系数的值源自在不同低雷诺数和高雷诺数测试场景下实现的最佳平衡。在实际应用中，SAS 项在狭窄的分离区域中激活，从而增加了比耗散率的生成，进而导致湍流粘度的上升。这种涡流粘度的增加有助于缓解流动分离。