物理学界最难的方程,描绘的竟是看似简单的日常现象。这个赏金高达百万美元的纳维-斯托克斯方程中,隐藏着哪些关于流体的奥秘?
物理学中包含了大量公式,它们描绘着物理学的种种现象,从宏观时空的延展到微观光子的碰撞。在所有这些公式中,有一组公式在数学上也极具挑战性,甚至被美国克雷数学研究所选作七个“千禧年大奖难题”之一,与庞加莱猜想、P=NP?等数学界的顶级难题并列,解决该问题的奖金高达100万美元。而这个物理界最难的公式,就是用于描述流体运动的纳维-斯托克斯方程。
最近,一项关于纳维-斯托克斯方程的最新研究得以发表。某种程度上,新的研究成果说明攻克这项千禧年大奖难题比预想的还要困难。为什么用数学理论阐明这组方程是如此困难,甚至相比之下,用于描述奇特黑洞的爱因斯坦场方程都显得更容易一些?
湍流,就是答案。这是一种再常见不过的现象。无论是在3万英尺高空飞行时颠簸的气流,还是家里浴缸出水口形成的漩涡,本质都是湍流。然而,熟悉的湍流却是物理世界中最难以理解的部分之一。
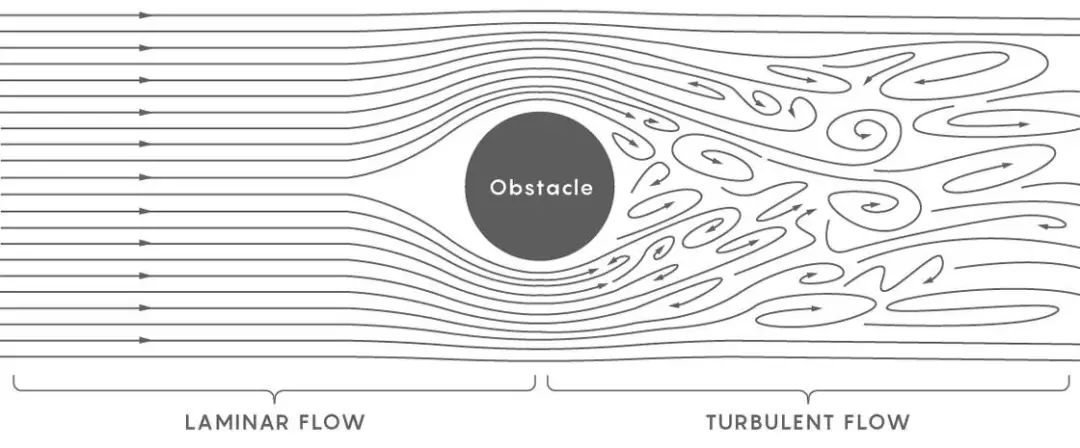
一条平稳流动的河流,是一个典型的无湍流体系,河流的每一部分以相同的速度运动。湍流则打破了这一规律,使得水流不同部分的运动方向和运动速率都不相同。物理学家将湍流的形成描述为:首先,平稳流动中出现一个涡流,这个涡流中会形成更多小涡流,小涡流进一步分化,使得流体被分解成许多离散的部分,在各自运动方向上与其他部分相作用。
科学家们希望理解的是,平流如何一步步瓦解成为湍流、已产生湍流的体系之后的形状是怎样演变的。但千禧年大奖悬赏的是更为简洁的问题:证明方程的解总是存在。换句话说,这组方程能否描述任何流体,在任何起始条件下,未来任一时间点的情况。
“第一步就是要尽力证明这些方程可以产生一些解,”来自普林斯顿大学的数学家CharlieFefferman说道,“尽管这并不能让我们真正理解流体的行为,但不这样做,就完全无法入手这个难题。”
如何证明那些解存在呢?首先可以考虑方程在什么条件下会“无解”。纳维-斯托克斯方程组涉及流速、压力等物理量的变化。数学家们关心的这样的情况:你在运算这组方程,经过有限的时间,系统中出现一个以无限速度运动的粒子。那样就会很麻烦:对于一个无限大的量,我们无法计算出它的变化。数学家们把这种情况称为“发散”(blowup)。在“发散”的情况下,方程失效,解也就不复存在。
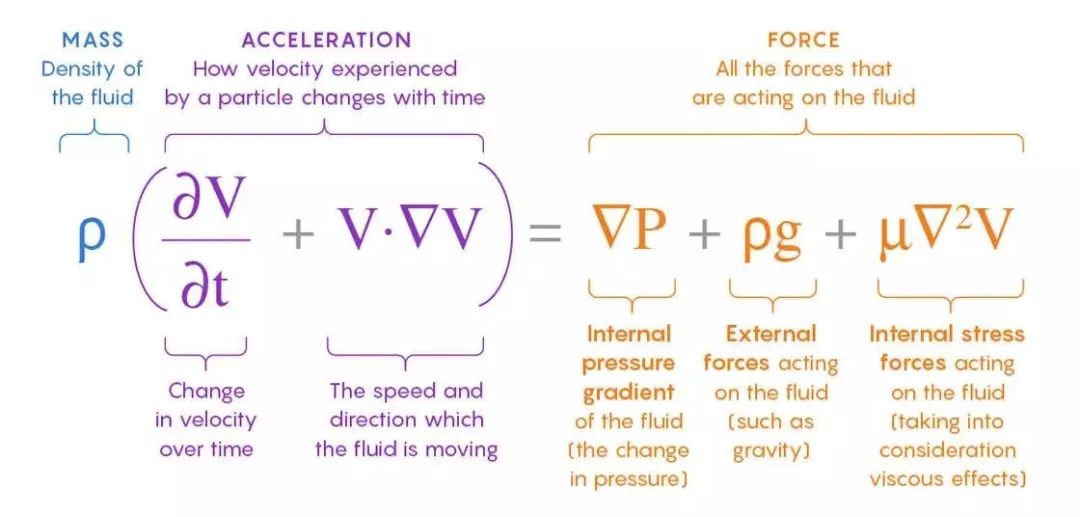
纳维-斯托克斯方程
证明“发散”的情况不会发生(或者说方程解总是存在),等同于证明流体中任何粒子的最大运动速率,被限制在某一有限的数值之下。相关物理量中,最重要的量是流体中的动能。
当我们用纳维-斯托克斯方程对流体建模,流体会具有一定初始能量。但是在湍流中,这些能量会聚集起来。原本均匀分散在流体中的动能,可能会聚集在任意小的涡流中,那些涡流中的粒子在理论上可以被加速到无限大的速度。
“当我的研究进入越来越小的尺度,动能对于方程解的控制作用则越来越弱。解可以是任意的,但我不知道如何去限制它。” 普林斯顿大学的VladVicol说到,他和Tristan Buckmaster合作完成了有关纳维-斯托克斯方程的最新工作。
根据方程失效的尺度,数学家们对像纳维-斯托克斯这样的偏微分方程进行分类。纳维-斯托克斯方程就处于分类谱系的极端。这组方程中的数学难度,某种意义上精确地反映出其所描述湍流体系的复杂程度。
“在数学角度看,如果你将某一点放大,那么就会失去解的部分信息,”Vicol解释说,“但是湍流的研究恰恰就是这样——动能从宏观传递向越来越小的尺度。所以,湍流的研究要求你不断地放大。
当谈及物理背后的数学公式,我们很自然地会想到:这会不会给我们研究物理世界的方式带来变革?纳维-斯托克斯方程和千禧年大奖引出的答案既是肯定也是否定的。经过近200年的实验,这些方程确实有效:由纳维-斯托克斯方程预测的流体流动与实验中观察到的流动总是相符的。如果你是一位物理学家,实验中这样的一致性或许已经足够。但数学家需要的更多——他们想要确定这组方程是否具有普遍性,想要精确捕捉流体的瞬时变化(无论何种初始条件),甚至去定位湍流产生的那个起点。
Fefferman说:“流体行为的诡谲总是令人惊叹。而那些行为理论上可以用这组基本方程来解释。它能很好地描述流体的运动。但是从方程描述流体运动到描述任意流体的真实运动,这一过程仍然未知。”
-
方程
+关注
关注
0文章
33浏览量
17085 -
物理学
+关注
关注
1文章
29浏览量
10052
原文标题:物理学最难的方程之一,解答奖金达100万美元
文章出处:【微信号:lianggezhizi,微信公众号:两个质子】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
比亚迪方程豹汽车6月销售18903辆
纳维塔斯与兆易创新携手开发高功率电源解决方案

文丘里效应方程的应用

锁相放大器在物理学中的应用

纳博特斯克紧凑型执行器AF系列产品介绍
神经网络理论研究的物理学思想介绍
方程豹汽车跨界演绎优雅硬派
无所不能的MATLAB|证明曲速引擎的物理学原理






 物理学最难的方程之一纳维-斯托克斯方程,解答奖金高达100万美金
物理学最难的方程之一纳维-斯托克斯方程,解答奖金高达100万美金












评论