利用C语言实现高斯列主元消去法解线性方程组

这篇文章主要是用C语言实现高斯列主元消去法求解多元一次方程。

高斯列主元消去法

由于涉及到的数学公式太麻烦了，所以从网上找了一张图片，介绍高斯消去法的，如下图:

Gauss列主元素法

示例

假如现在有一个三元一次方程组，如下图：

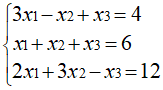
三元一次方程组

求解多元一次方程组可以分成三个步骤:

首先根据方程组构建增广矩阵

其次对增广矩阵经过行列式的初等变化变成上三角矩阵

最后从后往前回代求解。

构造增广矩阵

系数矩阵就是将方程组的系数组成矩阵。

而增广矩阵就是在系数矩阵的右边添上一列，这一列是线性方程组的等号右边的值。

下图即为行列式的增广矩阵：

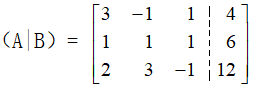
增广矩阵

组上三角矩阵

这里说的组上三角矩阵是指经过若干步初等变换，将矩阵左上角和右下角连线组成的对角线左下方的元素全部清零。

这个步骤主要涉及到主元以及初等变换两个概念。

主元指在消去过程中起主导作用的元素，主元通常选择绝对值最大的元素，用它做除法能够减小舍入误差的扩散，使得数值解比较可靠。

以下为行列式的初等变换：

换行变换:交换两行(列)

倍法变换:将行列式的某一行(列)的所有元素同乘以数k

消法变换:把行列式的某一行(列)的所有元素乘以一个数k并加到另一行(列)的对应元素上

而下面的图则是经过若干步初等变化组成的上三角矩阵:

迭代求解

在组成上三角矩阵之后，就可以从下往上依次回代求出方程的解了

C代码

#include
#include

#defineMAX_MATRIX10

/**
*@briefSwapRow进行行交换
*@paramm待计算的矩阵
*row待交行的行
*max_row待交换的另一行
*n矩阵行数
*/
staticvoidSwapRow(doublem[][MAX_MATRIX],introw,intmax_row,intn){
doubleswap;
for(intk=row;k<=?n;?k++)?{
????swap?=?m[row][k];
????m[row][k]?=?m[max_row][k];
????m[max_row][k]?=?swap;
??}
}

/**
?*?@brief?组上三角矩阵
?*?@param?m?待计算的矩阵
?*????????n?矩阵行数
?*/
static?void?SelectColE(double?m[][MAX_MATRIX],?int?n)?{
??int?max_row_e?=?0;??//主元所在行
??double?ratio?=?0;???//消元因数
??for?(int?j?=?0;?j?fabs(m[max_row_e][j])){
max_row_e=i;
}
}
if(max_row_e!=j){
SwapRow(m,j,max_row_e,n);//与最大主元所在行交换
}
//消元
for(inti=j+1;i=0;i--){
for(intj=i+1;j

	上述程序运行完成之后，终端输出：2.000000,3.000000,1.000000

	审核编辑：郭婷