傅里叶级数有时移特性
傅里叶级数是指将周期函数分解为一系列正弦函数和余弦函数的和的表达式。它得名于法国数学家傅里叶,被广泛应用于信号处理、图像处理、噪声分析等领域。傅里叶级数的最重要的特征之一就是时移特性。在本文中,我们将介绍傅里叶级数的时移特性以及它在实际应用中的作用。
一、傅里叶级数基础
傅里叶级数可用于表示具有周期性的函数。 周期函数可以表示为正弦函数和余弦函数的和的形式,如下所示:
$$ f(x) = \frac{a_0}{2} + \sum_{n=1}^{\infty}(a_n{cos~n\omega}x+b_n{sin~n\omega}x) $$
其中,$\omega$ 是频率,$a_n$ 和 $b_n$ 是函数 $f(x)$ 的傅里叶系数。傅里叶系数可以通过对 $f(x)$ 进行积分来计算,具体如下:
$$ a_n=\frac{2}{T}\int_{-T/2}^{T/2}f(x){cos~n\omega}x\ dx, $$
$$ b_n=\frac{2}{T}\int_{-T/2}^{T/2}f(x){sin~n\omega}x\ dx $$
其中 $T$ 是函数 $f(x)$ 的周期。
二、傅里叶级数的时移特性
傅里叶级数的时移特性是指在时间轴上对函数进行平移,它仍可以表示为一系列正弦函数和余弦函数的和。 如果我们将函数 $f(x)$ 平移 $a$ 个单位(即 $f(x-a)$),则其傅里叶级数可以表示为:
$$ f(x-a) = \frac{a_0}{2} + \sum_{n=1}^{\infty}(a_n{cos~n\omega}(x-a)+b_n{sin~n\omega}(x-a)) $$
我们可以将傅里叶系数展开后得到:
$$ a_n=\frac{2}{T}\int_{-T/2}^{T/2}f(x-a){cos~n\omega}x\ dx, $$
$$ b_n=\frac{2}{T}\int_{-T/2}^{T/2}f(x-a){sin~n\omega}x\ dx $$
这说明傅里叶系数中只是函数 $f(x)$ 中的自变量 $x$ 发生了变化,而其他部分保持不变。 因此,平移不会改变傅里叶系数的值,而只是改变了自变量的值。 因此,傅里叶级数具有时移的特性。
三、时移的应用
傅里叶级数的时移特性在信号处理和图像处理等领域中得到了广泛的应用。在这些领域中,我们通常需要将信号或图像进行平移,以便进行分析或处理。 在这种情况下,我们可以使用傅里叶级数,而无需重新计算傅里叶系数。
例如,图像处理中的图像对齐需要将两幅图像平移,使它们对齐。 如果我们需要对齐的两幅图像的频谱是已知的,那么我们只需移动频谱图像,而无需重新计算它们的傅里叶系数。
除此之外,时移特性还被广泛运用于测量信号的延迟。通过对信号进行逆傅里叶变换,可以获得函数在时间域中的表示,并通过平移进行信号的延迟测量。
四、总结
傅里叶级数具有时移特性,因此我们可以在函数 $f(x)$ 平移时,使用原有的傅里叶系数,而无需重新计算。这种特性在信号和图像处理中有重要的应用,可以简化许多分析和处理任务。通过使用傅里叶级数的时移特性,我们可以更加高效地工作并取得更好的结果。
-
图像处理器
+关注
关注
1文章
105浏览量
15978 -
信号处理器
+关注
关注
1文章
258浏览量
25842 -
傅里叶变换
+关注
关注
6文章
443浏览量
43219
发布评论请先 登录
VirtualLab:光栅的优化与分析
VirtualLab 应用:薄元近似(TEA)与傅里叶模态法(FMM)的光栅建模
漫画傅里叶解析-[日]涉谷道雄
VirtualLab Fusion应用:利用空间滤波器“清理”激光束
VirtualLab Fusion应用:非近轴衍射分束器的设计与优化
VirtualLab Fusion应用:光波导的入射耦合和出射耦合区域
VirtualLab Fusion案例:单分子显微镜高NA成像系统的建模
VirtualLab Fusion案例:高NA傅里叶单分子成像显微镜
低压配电中产生的谐波应该如何治理?
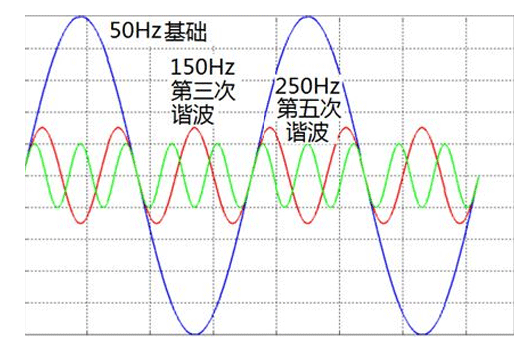





 傅里叶级数有时移特性
傅里叶级数有时移特性











评论