在上期中,我们介绍了最新一期《模拟设计期刊》的亮点内容。
本期,为大家带来的是《如何确保有源 EMI 滤波器的稳定性和性能》,将讨论如何采用适当的补偿和阻尼技术实现有源电磁干扰滤波器 (AEF)的稳定性和出色性能。
引言
作为昂贵的传统大型无源滤波器的出色替代品,有源电磁干扰滤波器 (AEF)可以帮助设计人员应对不断增加的 EMI 挑战、提高功率密度以及降低电源解决方案的成本。
大多数 AEF 使用基于运算放大器的有源电路来检测噪声并注入适当的消除信号以降低 EMI,例如LM25149-Q1中集成的AEF。为了使用这种 AEF 实现出色性能,运算放大器电路需要保持稳定且运算放大器应处于非饱和状态。否则,AEF 的性能会更差,甚至可能会在系统中注入额外的噪声。本文将探讨如何采用适当的补偿和阻尼技术实现 AEF 的稳定性和出色性能。
AEF 补偿
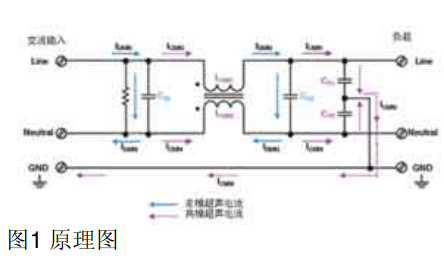
图 1 (a) 显示了一个无补偿的 AEF。在图 1 中,VS是噪声源,ZS是内部阻抗,ZL是线路阻抗稳定网络或电源的阻抗,Cin是电源转换器的输入电容器,L 是差模电感器,Csense和 Cinj是感应电容器和注入电容器,RDC_fb为 Op_amp 提供直流反馈,Cpara是电源布线和接地之间的寄生电容。
作为一个基于运算放大器的反馈电路,图 1 (a) 中的 AEF 会变得不稳定,进而导致运算放大器饱和。在这种情况下,AEF 的性能会受到显著影响,并且 AEF 可能会消耗更多功率并在系统中注入额外的噪声。由于运算放大器的负载网络很复杂,图 1 a 中的 AEF 在低频和高频下都会不稳定。
在低频(例如在 10 kHz 与 50 kHz 之间)下,环路增益的相位会变为正 180 度,系统会变得不稳定,造成这种问题的主要原因是 Cinj与 L 以及 Csen与 RDC_fb形成了分压器。低频补偿的一种方法是添加 Rcomp和 Ccomp与 RDC_fb并联,如图 1(b) 所示。Ccomp通过使反馈网络在低频下具有容性来进行低频补偿。Rcomp用于确保 AEF 的性能。此外,转换器的输入端通常用电解电容器来存储能量并确保转换器稳定。电解电容器的等效串联电阻 (ESR) 也有助于提高低频稳定性。
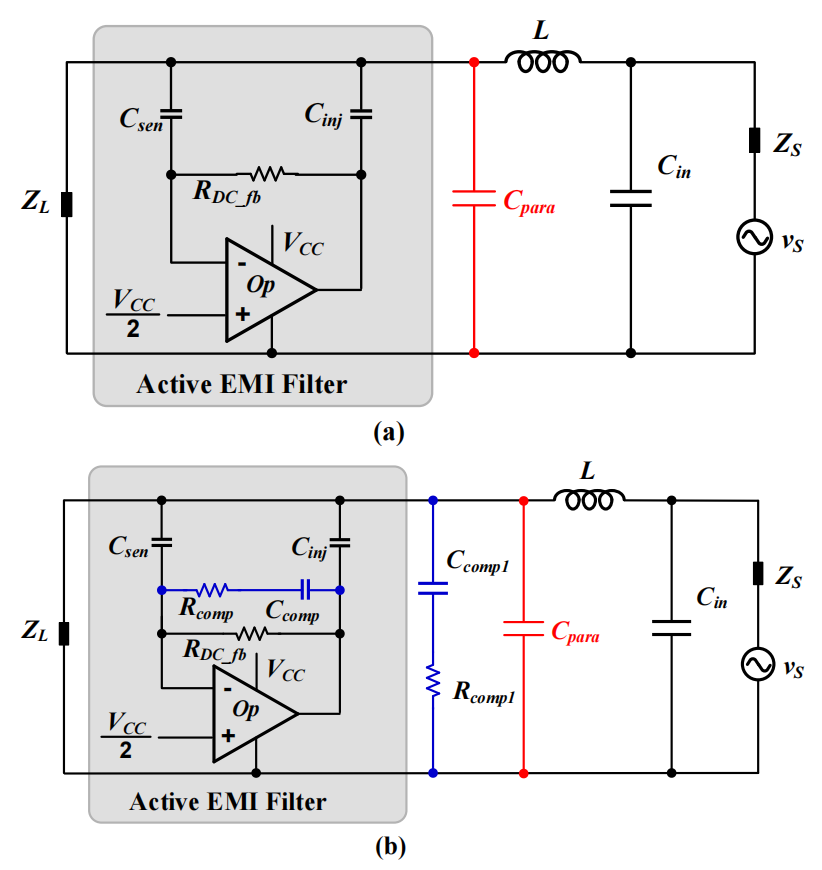
图 1:无补偿的 AEF (a);有补偿的 AEF (b)
在高频下,运算放大器和 Cpara的输出阻抗会产生一个极点,造成环路增益的相位滞后。此外,运算放大器通常具有低频极点。因此,环路增益在高频下将具有两个极点且其相位接近负 180°,这会导致在高频下不稳定。Rcomp1和 Ccomp1(图 1(b) 中)用于高频补偿,大小为 100 nF 和 0.5Ω。Rcomp1和Ccomp1可以增加高频下环路增益的相位,使系统具有足够的相位裕度来保证高频稳定性。在某些应用中,高频陶瓷电容器(例如 10 nF 或 100 nF)对于高频噪声过滤或对于保护电路(例如用于反向保护的智能二极管)而言是必不可少的。在此类情况下,有几种方法可以保持高频稳定性:
? 在检测/注入节点和高频陶瓷电容器之间插入铁氧体磁珠以将它们解耦。
? 添加与高频电容器串联的小电阻器以进行补偿。
? 将高频电容器放置在远离AEF的位置,因为陶瓷电容器和印刷电路板布线的ESR和等效串联电感 (ESL)也有助于提高高频稳定性。
总体而言,必须确保检测/注入节点对地的阻抗不受高频(10 MHz 至 50 MHz)电容控制。
AEF 阻尼
由于热变化或开关抖动,电源转换器可能会在低于开关频率的频率下产生噪声(在本文中被称为低频干扰)。对于图 1 (b) 中的 AEF,方程式 1 将其等效阻抗表示为:
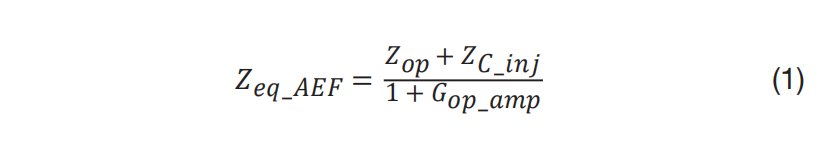
方程式 1
其中,Zop和 Gop_amp是输出阻抗和从检测节点到运算放大器输出端的电压增益,而 ZC_inj是注入电容器的阻抗。
根据方程式 1,图 1 (b) 中的 AEF 的等效阻抗在低频下具有容性。因此,AEF 会在低频(例如在 10 kHz 到 100 kHz 之间)下与差模电感器 L 发生谐振。考虑到这种谐振,低频干扰会使运算放大器输出电压和输出电流较大。由于运算放大器的输出摆幅和输出电流能力有限,运算放大器会进入非线性区域甚至达到饱和状态,这可能会影响 AEF 性能并导致 AEF 向系统中注入额外的噪声。
处理这一问题需要抑制谐振。图 2 显示的两种阻尼方法使 AEF 在谐振频率下具有较小的电容。在图 2 (a) 中,阻尼电阻器 Rdamp被插入到注入路径中。这样,Rdamp越大,谐振阻尼越佳。然而,插入阻尼网络后,方程式 2 将 AEF 的等效阻抗表示为:
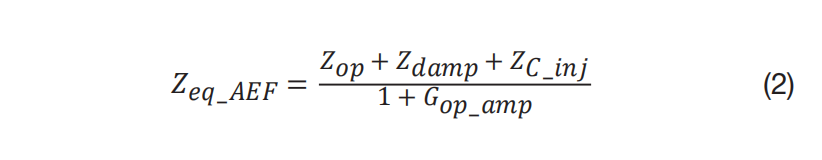
方程式 2
其中,Zdamp是阻尼网络的阻抗。
较大的 Rdamp会增加 Zeq_AEF,从而影响 AEF 的性能。所以这种阻尼方法主要适用于高频开关转换器,比如 2 MHz 的开关转换器。为了有效抑制谐振,品质因数应在 1 左右或以下。若要使品质因数接近 1,请在计算 Rdamp时采用方程式 3:
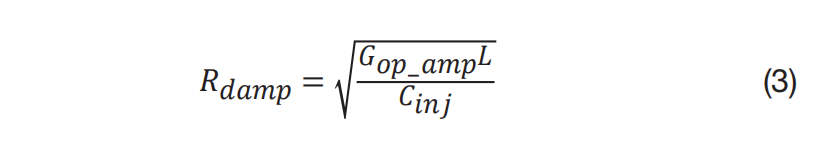
方程式 3
为了提高图 2 (a) 所示的 AEF 的性能,请将电容器 Cdamp与阻尼电阻器 Rdamp并联,如图 2 (b) 所示。在谐振频率下,电阻器 Rdamp将控制阻尼网络的阻抗以抑制谐振。在 AEF 需要进行噪声衰减的高频下,电容器 Cdamp将控制阻尼网络的阻抗,从而确保 AEF 的性能。方程式 4 和方程式 5表示了一个用于谐振阻尼的良好 Rdamp和 Cdamp组合:
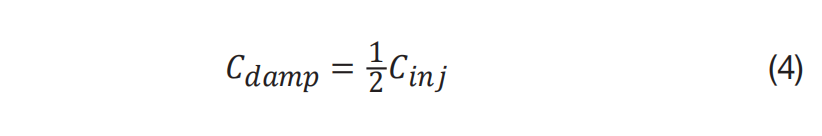
方程式 4
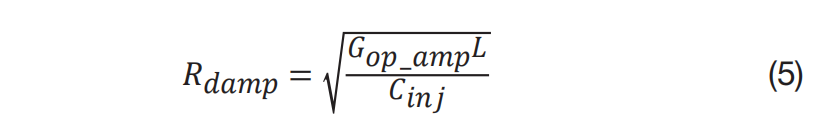
方程式 5
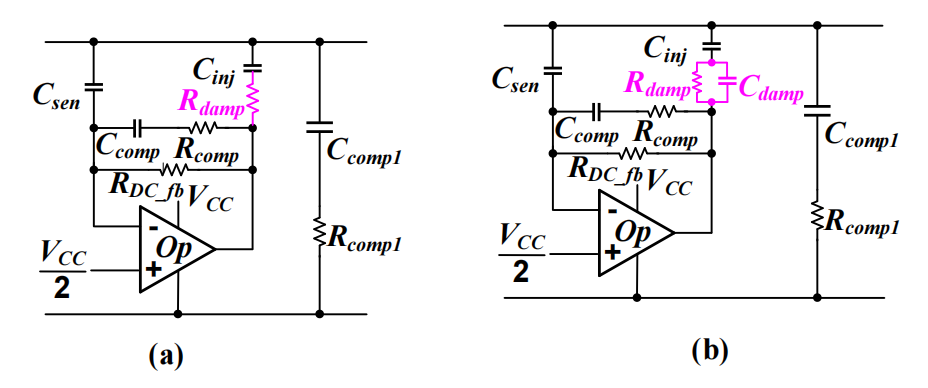
图 2:抑制差模电感器和 AEF 谐振的方法:电阻器阻尼 (a);电阻器和电容器并联阻尼 (b)
图 3 显示了 400 kHz 降压转换器在 10 kHz 至 1 MHz 范围内的频谱测试结果(对应于 AEF 关闭、AEF 开启但无阻尼、AEF 开启且有电阻器-电容器并联阻尼的情况),其中基于方程式 4 和方程式 5 选择 Rdamp和 Cdamp。在图 4 中无阻尼的情况下,谐振会在大约 30 kHz 处出现尖峰,这会影响 AEF 性能并使本底噪声增加。使用阻尼网络后,谐振尖峰现在位于 45 kHz 处,但其幅度大大降低,这意味着已成功抑制谐振。因此,AEF 有效地抑制了高频噪声,并且本底噪声大幅降低。
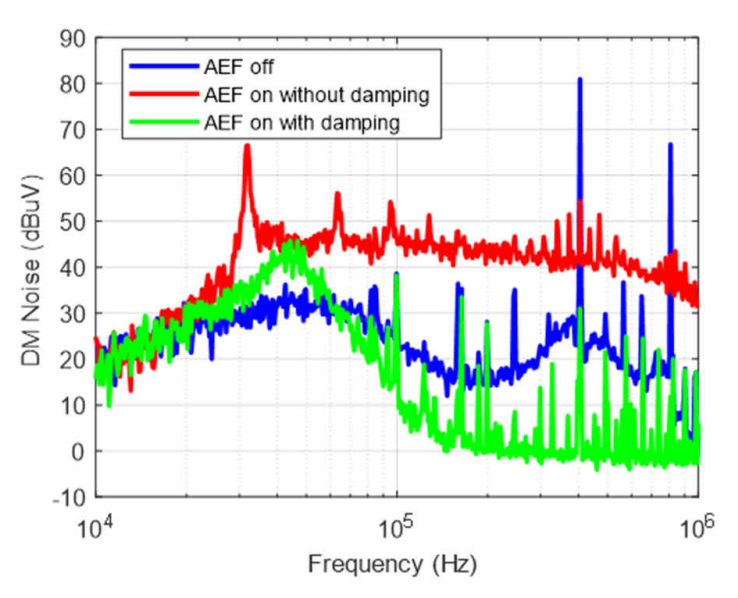
图 3:有阻尼和无阻尼的测试结果
同时具有补偿和阻尼特性的 AEF 性能
通过进行适当的补偿和阻尼,AEF 可以实现显著的降噪效果,如图 4 所示。测量结果是使用 440 kHz 电源转换器获得的,输入电压为 12V,输出为 5V/5A。AEF 和转换器均采用LM25149-Q1实现。L 为 1?H,Csense为 100 nF,RDC_fb为 50 kΩ,Cinj为 470 nF。针对补偿,低频补偿采用 1 kΩ Rcomp和 1 nF Ccomp,高频补偿采用 0.5 Ω Rcomp1和 100 nF Ccomp1。
针对阻尼,使用的是电阻器和电容器并联阻尼;Rdamp为 15 Ω,Cdamp为 220 nF。如图 4 所示,AEF 在 440 kHz 下可实现约 50 dB 的噪声衰减。与性能类似的无源滤波器相比,尺寸可以缩小约 50%,体积可以缩小约 75%。
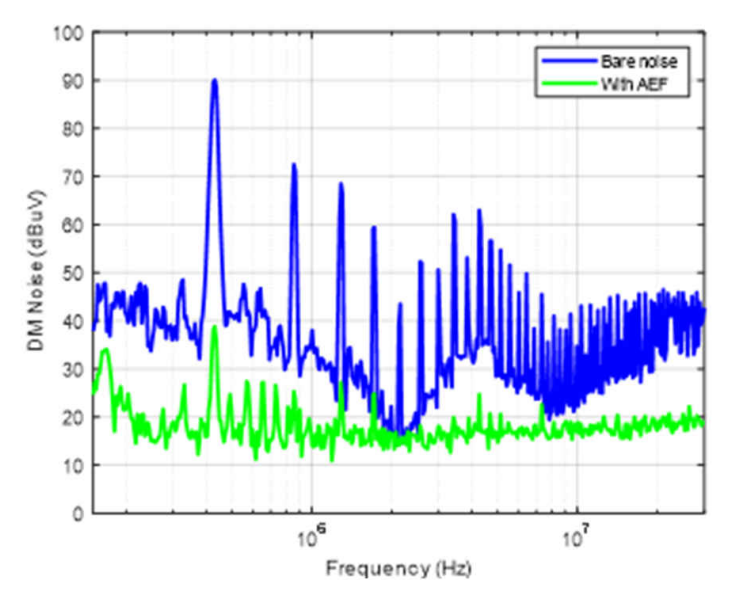
图 4:进行适当补偿和阻尼的 AEF 的降噪情况
结论
补偿和阻尼对于实现良好的 AEF 性能至关重要。本文讨论的方法都可以通过LM25149中集成的 AEF 轻松实现。通过采用适当的补偿和阻尼,AEF 可以实现显著的降噪效果。电力电子设计人员应该利用 AEF 来实现更高的功率密度、更高的效率和更低的成本。
-
滤波器
+关注
关注
162文章
8181浏览量
183112 -
运算放大器
+关注
关注
217文章
5763浏览量
177948 -
emi
+关注
关注
53文章
3824浏览量
132316 -
电磁干扰
+关注
关注
36文章
2410浏览量
106993
原文标题:模拟芯视界 | 如何确保有源 EMI 滤波器的稳定性和性能
文章出处:【微信号:tisemi,微信公众号:德州仪器】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
电磁干扰滤波器的设计和选用分析
电磁干扰滤波器的资料概述





 如何实现有源电磁干扰滤波器的出色性能
如何实现有源电磁干扰滤波器的出色性能












评论