一文详解单粒子效应的电荷收集

文章来源：学习那些事

原文作者：前路漫漫

本文介绍了单粒子效应中电荷收集的三个阶段、聚集过程和扩散过程。

在探讨单粒子翻转基本机理时，深入理解并掌握各类电荷收集过程及其作用机理至关重要，这些过程与机理对明确单粒子效应特征、开展相关试验数据分析具有重要参考价值。针对上述机理，已有研究者开展了系统性分析，本文将梳理核心结论，为试验结果分析提供基础理论支撑。

电荷收集的三个阶段

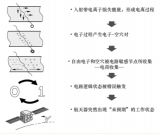
相关研究证实，单粒子效应的电荷收集过程主要包含三个阶段：一是电子-空穴对初始分离的漂移过程，二是受电场调控的聚集过程，三是PN结耗尽层外区域载流子的扩散过程。图1(a)为电荷收集过程示意图，从图中可观察到，不同位置的电荷收集方式存在差异，且各过程的时间响应特性也不相同。由于不同电荷收集过程的时间响应存在显著区别，它们均是晶体管级、存储单元及存储单元邻近区域单粒子效应建模分析中需明确的基础物理过程。

围绕离子撞击后电路中的电荷收集基本特性，学界已开展大量试验与理论研究。试验研究层面，研究者通过宽束电荷收集谱测量、粒子微束与激光微束诱发电荷收集脉冲测量等手段展开探索；在电荷收集特性分析中，电路数值仿真方法也被用于揭示电荷收集的物理过程。

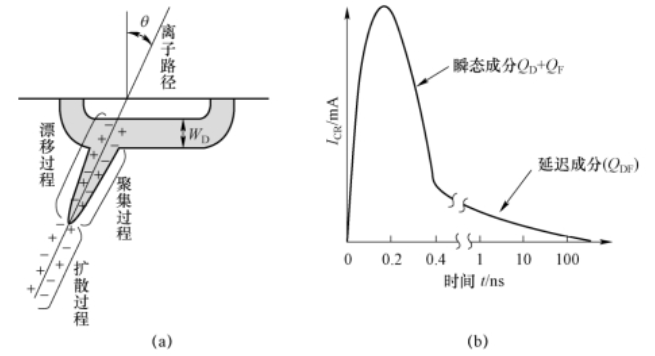
已知当带电离子撞击电子器件或集成电路时，从带电粒子诱发电荷收集的角度来看，最敏感的区域是通常处于反偏状态的PN结近区。PN结耗尽层内存在高电场，该电场会对诱发的载流子（电荷）产生漂移与聚集作用，使得敏感节点的电荷收集效率大幅提升。敏感节点收集电荷后，会形成如图1(b)所示电流脉冲的瞬态成分（Q?+Q?）；当离子穿越至PN结耗尽层近区时，其产生的载流子通过扩散过程到达耗尽层场附近后，同样会被敏感节点有效收集，进而形成如图1(b)所示电流脉冲的延迟成分Q?。即便带电离子直接撞击远离耗尽层的区域，电离产生的载流子仍可通过扩散过程被PN结节点收集，最终形成脉冲电流。

在电子器件与集成电路单粒子翻转现象被发现后不久，美国IBM公司的研究者借助数值模拟方法，探究了反偏PN结对入射α粒子撞击的响应机制。该研究的重要发现之一是PN结静电电位存在扰动现象，即“电场聚焦”过程。此过程通过将静电场分布从结近区延伸至衬底区域，显著增加了电荷收集量，也是敏感节点电荷聚集收集的直接诱因，关于电荷收集的聚集过程将在下文详细说明。

电荷收集的聚集过程

如前文所述，在带电离子引发的电子-空穴对电荷收集过程中，存在一种电荷聚集现象（又称“漏斗效应”），该现象是单粒子效应电荷收集的核心过程之一。其最初在粒子诱发单粒子翻转机理研究中被发现，后续在其他类型粒子的单粒子效应机理研究中得到了广泛验证。在早期α粒子单粒子效应基本机理研究中，研究者发现PN结敏感区实际收集的电荷量，远高于通过漂移与扩散运动预计的收集量，基于此提出了全新的电荷收集模型——电荷聚集模型。

图2为电荷聚集过程的示意图。当N?P结施加正向偏压V_B后，会形成电子浓度为N_D的耗尽层。当α粒子垂直注入时，会形成半径约1000 ?的电子-空穴对等离子体径迹[如图2(a)所示]。此时，等离子体的密度较衬底掺杂浓度高出数个数量级，可达10??~10??cm??；根据相关计算分析，能量为275 MeV的铁离子产生的电子-空穴对密度可达5.5×10??cm??。

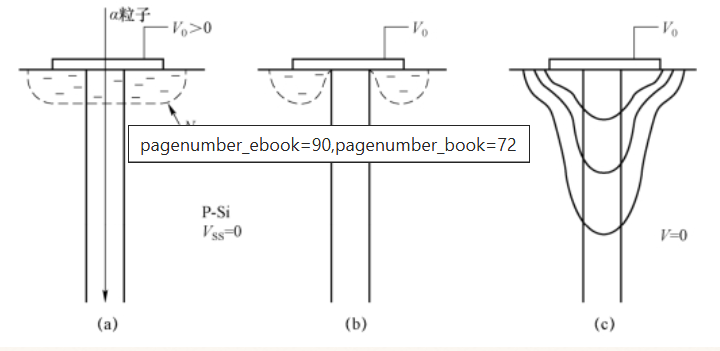
在这一瞬时，等离子体周围的耗尽层会发生电中性化[如图2(b)所示]；随着耗尽层区域进一步消失，其对电场的屏蔽作用减弱，正向偏压V_B产生的电场等位线分布会向衬底内部延伸[如图2(c)所示]，正是这种电场延伸现象，直接诱发了电荷聚集过程。

在电荷收集过程中，电子-空穴对等离子体通过两种形式实现电荷分离，即径向分离与纵向分离。初始阶段，由于等离子体局部密度较高，分离过程以径向为主：在径向电场作用下，空穴被驱送至衬底区域，而电子则保留在等离子体径迹附近。同时，在纵向电场作用下，已分离的电子会向上漂移，并被N?电极收集。

随着等离子体密度逐渐降低，PN结的耗尽层开始重新形成，且形成过程从等离子体径迹外表面逐步向中心推进。此阶段，电荷分离以纵向为主，电子持续被N?电极收集，而空穴则逐渐脱离纵向电场的影响，直至结耗尽层完全恢复。整个电荷收集过程速度极快，通常认为耗时小于1 ns，远快于仅依靠扩散过程的电荷收集速度。

本质上，电荷聚集过程是耗尽层电场向中性衬底区域重新分布的过程，该过程最终使得离子穿越的敏感节点能够收集到更多电离产生的电荷。

机理分析

但在静态电路中，以静态存储器（SRAM）为例，其处于反偏状态的晶体管与外部有源电路直接相连，这使得电荷聚集过程的表现并不显著。原因在于，当电路敏感节点受到离子撞击后，其反偏电压可能会消失，进而使得漂移收集与聚集收集过程的电荷贡献大幅下降。

电荷聚集效应可显著提升敏感节点的电荷收集量。当重离子撞击敏感节点时，会沿带电离子的运动路径诱发敏感节点电场向衬底区域延伸；在此作用下，敏感节点周边一定距离内沉积的电荷，可通过高效漂移过程被敏感节点收集，这一现象便是电荷收集的聚集效应。学界已对该过程展开深入研究，其中McLean与Oldham提出的聚集效应分析模型，为早期理解电荷收集过程的特征提供了关键支撑。后续研究进一步探究了外延层衬底对瞬态电荷收集特性的影响，不仅明确了电荷聚集收集的更多特征，还对电荷通过衬底的聚集收集过程展开了全面分析，相关细节可参考具体文献。

在部分电路结构中，通过维持偏置电压稳定以实现PN结隔离，这一操作对电荷收集过程具有重要影响。例如在静态SRAM电路中，电荷聚集过程对单粒子翻转的影响较弱，核心原因是反偏状态晶体管的结与动态外部电路相连。在此场景下，离子撞击节点的偏压无法保持稳定，实际会在零偏压与反偏电压之间频繁波动；而撞击节点电压突然降至零偏压的情况，会削弱电荷漂移收集的效果，电荷聚集收集的效率也会随之下降。因此，电荷聚集收集仅在电路响应初期发挥一定作用，进入响应后期后，电荷收集的主导过程则转变为扩散收集。

电荷收集的扩散过程

从时间维度分析，当强电场主导的电荷快速漂移过程结束后，电荷收集的主导过程会转变为速度更慢的扩散过程。扩散过程的电荷收集量与离子撞击位置密切相关：当撞击点靠近漏极敏感节点时，扩散收集的电荷量较多；若撞击点远离漏极敏感节点，扩散收集的电荷量则会减少。若撞击点未设置保护阱作为限制边界，扩散过程的电荷收集范围甚至可能超出器件正常特征尺寸（Smith 1995），且该现象在现代电子器件与集成电路中愈发显著。

为充分理解扩散过程的电荷收集机制，进而在器件工艺与加固设计中制定针对单粒子效应的有效缓解措施，需先掌握带电离子的径迹结构特征。为帮助理解电荷收集过程，图3展示了带电离子在半导体MOS管结构中产生电荷及收集过程的二维结构示意图，图4则呈现了晶体管单元中重离子电离径迹内电子-空穴对的密度分布示意图。

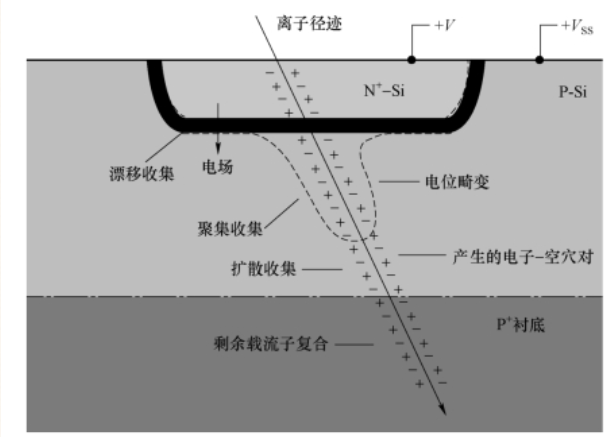
带电离子径迹结构的长度通常小于或等于离子射程长度；在分析电荷收集的扩散过程时，若聚焦于高密度等特殊条件，并设定特定边界条件成立，便可对扩散过程展开简化分析。

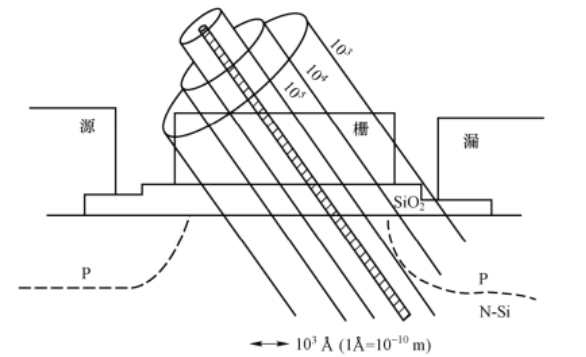
尽管早在1983年，学界就已报道扩散过程在电荷收集中的重要作用，但当时尚未意识到漂移与扩散的相互关系可用于简化电荷收集过程的分析。由于施加电压为反向偏压，在高密度条件下，衬底电场强度会达到使少数载流子漂移电流近似等于少数载流子扩散电流的水平，因此总电流约为扩散电流的两倍。该结论的依据在于：扩散区域体区（DRB）在一定程度上可近似为静态，能够阻碍多数载流子电流；这表明在DRB处，多数载流子的漂移电流与扩散电流绝对值大致相等。

在高密度条件下（载流子密度远高于衬底及DRB处的掺杂密度，该情况常见于离子轨迹区域），电子-空穴对密度几乎仅随位置变化（即DRB处的载流子密度值与密度梯度近似相等），因此电子-空穴对的漂移电流与扩散电流均取决于载流子迁移率。由此可知，DRB处多数载流子的漂移电流与扩散电流相等，这也意味着此处少数载流子的漂移电流与扩散电流同样相等；但与多数载流子不同的是，少数载流子的两种电流会相互叠加而非抵消，因此DRB处的总电流为少数载流子扩散电流的两倍。

但这一结论并非电荷收集的唯一决定因素：扩散电流与载流子密度函数的梯度成正比，而载流子密度函数本身又受电场影响，因此电场仍会间接作用于扩散电流。需注意的是，即便通过简化得出“总电流为扩散电流两倍”的结论，实际电流大小仍受整个器件电位分布的影响。

不过，通过其他简化方式可更便捷地估算高密度条件下的扩散电流。稳态分析结果显示，衬底可划分为两个准中性区域，且每个区域具备特定的简单特性。衬底下方区域会耗尽多余载流子，同时承担大部分衬底电压的施加；由于该区域电导率较低（相较于上方高密度区域）且存在较大压降，因此被定义为高电阻区（HRR）。强电场会阻碍少数载流子进入该区域，而准中性特性则确保多数载流子不会出现过量积累。该区域具有自我维持特性：低电导率会催生强电场，而强电场又会进一步维持低电导率状态。计算机仿真结果表明，瞬态条件下也存在类似现象——在此场景中，HRR位于离子径迹下方；若径迹长度足够长以抵达下电极，其下端会被快速清除，进而形成HRR。该区域在电位分布图中可清晰识别，从中可观察到大部分衬底电压通过径迹下方低电导率区域，而沿离子径迹分布的电场则相对较弱；载流子密度图中同样能观测到该区域，说明此处不存在载流子向下扩散的现象。

HRR上方的衬底区域呈现弱电场与高载流子密度的特征，而这些正是双极扩散方程的适用条件，因此该区域被命名为双极区（AR）。需注意的是，双极扩散方程仅描述载流子密度函数（未涵盖包含漂移的载流子流），并非表明载流子运动由扩散主导。在相同的密度梯度条件下，不同大小的漂移辅助电流密度可与同一载流子密度函数兼容；当密度梯度为零时，离开某一体积单元的载流子会被其他移动单元的载流子补充，这种流动形态可在不改变载流子密度函数的前提下叠加到另一个单元中，也就是说，不同的载流子流型可与相同的载流子密度函数共存。具体而言，电子与空穴可呈现完全不同的运动方向（例如一种载流子向上移动，另一种则向下移动），这意味着同一过剩载流子密度函数可适用于准中性区中的两种载流子。

由此可见，双极扩散方程与漂移电流的存在并不冲突；即便在弱电场环境下，高密度电离径迹上也能产生强漂移电流。尽管双极扩散方程未直接描述载流子电流，但它能够刻画载流子密度函数；结合“总电流为少数载流子扩散电流两倍”的结论，便可计算出载流子流的具体大小。不过，仅依靠方程无法完成计算，还需明确相应的边界条件。该方程仅适用于AR区域，因此需确定AR边界的具体位置，同时明确这些边界处的过剩载流子密度。靠近HRR的AR下边界处，过剩载流子密度的边界值较为简单（即数值为零），但边界位置的计算难度较大，这是因为它会受到衬底压降等多种因素的影响——衬底压降越大，通常会导致HRR宽度增加，而AR宽度则相应减小。不过，在假设的高密度条件持续的初始阶段，若合理选择部分边界条件，总电流可近似视为双极扩散方程预测的扩散电流的若干倍。