射频技术的故事,要从麦克斯韦和他的方程组讲起。对很多行业的人来说,麦克斯韦这个名字或许有些陌生—— 他的名气似乎远不及电学领域的安培、法拉第,也比不上发明大王爱迪生、交流电先驱特斯拉。但对每一个射频人而言,他却是不折不扣的 “祖师爷”:是他第一个预言了电磁波的存在,第一个将电与磁的规律统一成完整体系,第一个揭示了电磁波与光的统一性,更是我们如今这个无线通信时代的 “奠基者”。所以,当我们刷着抖音、玩着王者,享受无线连接带来的便利时,别忘了背后站着这位用方程点亮无线世界的先驱 —— 麦克斯韦。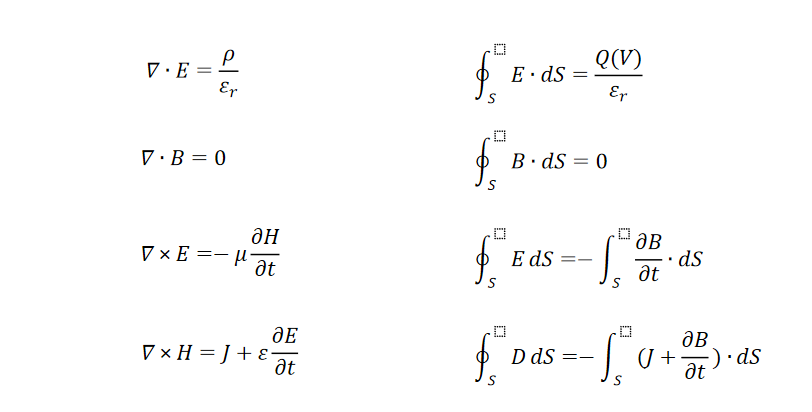
图1 麦克斯韦和麦克斯韦方程的微积分形式
麦克斯韦方程组,就是图 1 里的那两组公式:左边是微分形式,右边是积分形式。对不少 “高等数学恐惧症” 患者来说,这组方程简直是 “劝退现场”—— 微积分符号看得人头晕,那个倒三角▽像个神秘符号,中间带圈的符号更是让人摸不着头脑。我当初也一样:公式里的 E、B、ρ 这些字母代表什么意思还能看懂,但前面的符号是啥?它们又在表达什么规律?
直到朋友圈里两篇爆文的出现,才让我对这组方程有了新的认识——《最美的公式:你也能懂的麦克斯韦方程组(微分篇)》《最美的公式:你也能懂的麦克斯韦方程组(积分篇)》。那阵子,这两篇文章几乎刷爆了所有射频人的朋友圈:原来祖师爷留下的 “硬核知识”,也能被解读得这么通透易懂?于是我也跟着 “啃起了硬骨头”,拼命查资料、翻论文,甚至把麦克斯韦当年的三篇经典著作都翻了出来 ——《论物理力线》(1861)、《电磁场的动力学理论》(1865)、《电磁学通论》第二卷(1873 年,牛津大学克拉伦登出版社)。坦白说,这些一百多年前的文字读起来并不容易:古英语的表述方式、略显晦涩的推导逻辑,越读越觉得自己像在 “啃天书”
但或许,我们可以换个角度:先抛开那些复杂的运算符号,从物理意义入手理解麦克斯韦方程组,会不会更容易些?
先看第一个方程。不管是微分形式还是积分形式,左边都是对电场 E 的操作,右边则是和电荷相关的量 —— 微分形式里是电荷密度 ρ,积分形式里是总电荷 Q。说白了,它描述的就是电场和电荷的关系。这一点,很多中学生都能脱口而出:电荷会产生电场。理解了这层,再看微分和积分形式就简单了:微分,就像把一个大物体切成无数小块,看每一小块的电场与电荷的关系;积分,则是把这些小块 “拼” 回去,看整个封闭曲面内的总电场与总电荷的关系。所以麦克斯韦方程组第一个方程的微分形式,说的是 “当我们观察一个无限小的封闭曲面时,电场的特性由这一小块空间里的电荷密度 ρ 决定”;积分形式则是 “某个封闭曲面内的电场总和,等于这个曲面里包含的总电荷量”。更进一步说,电场是 “有源的”,而产生它的 “源”,就是电荷。这其实就是我们中学学过的 “电场高斯定律”,是库伦定律的延伸。配合图示理解,这种 “电荷生电场” 的关系会更清晰。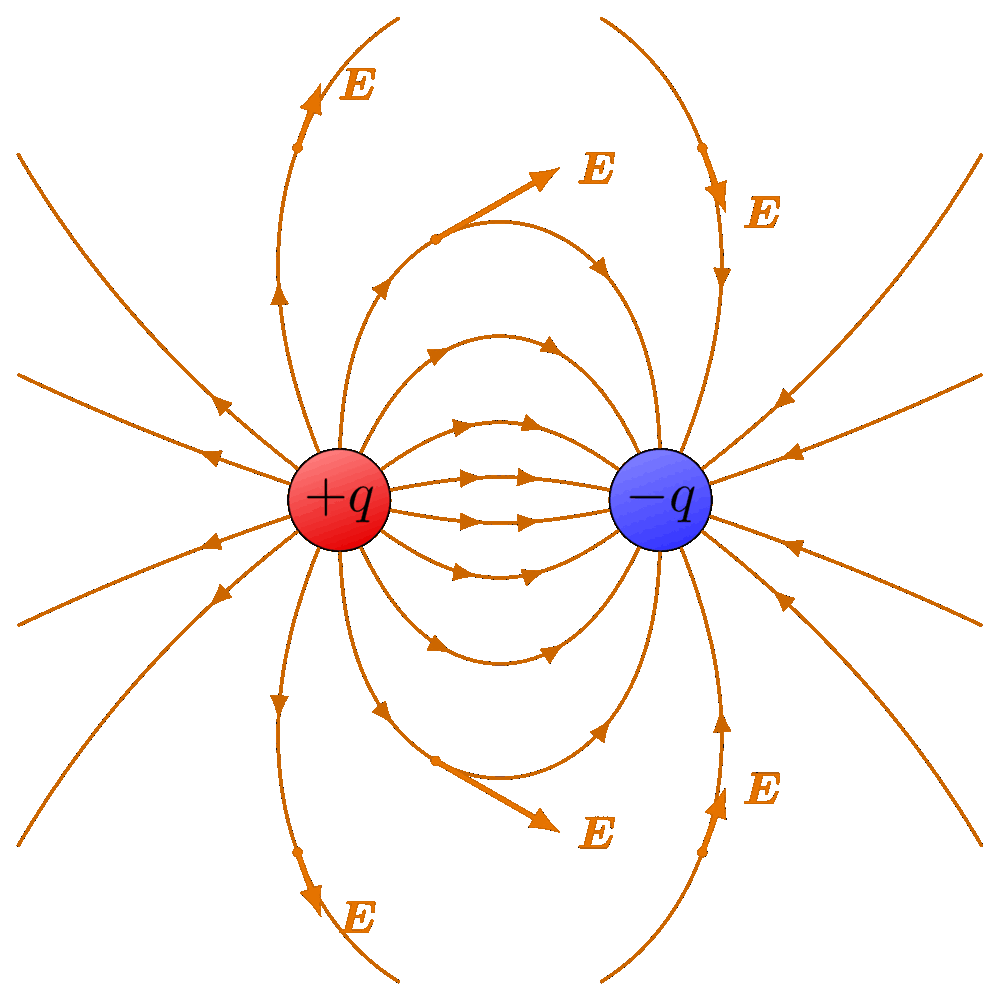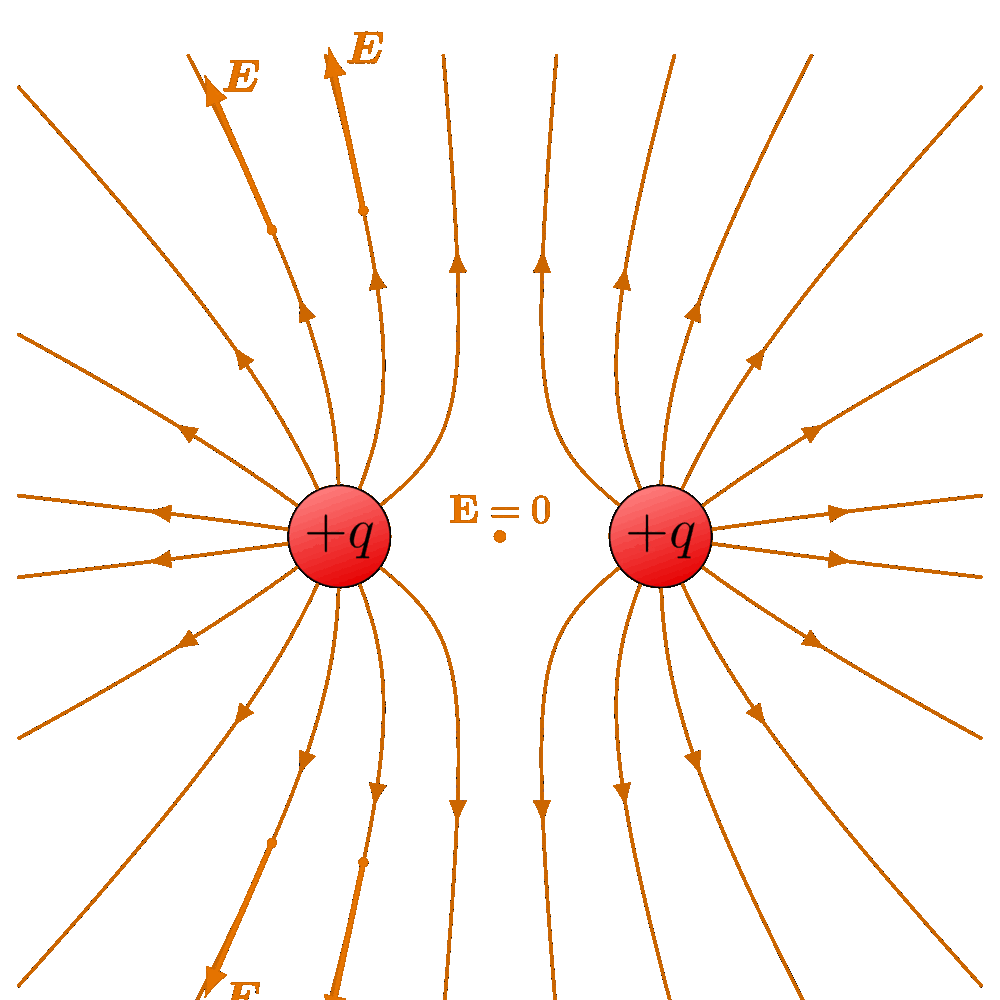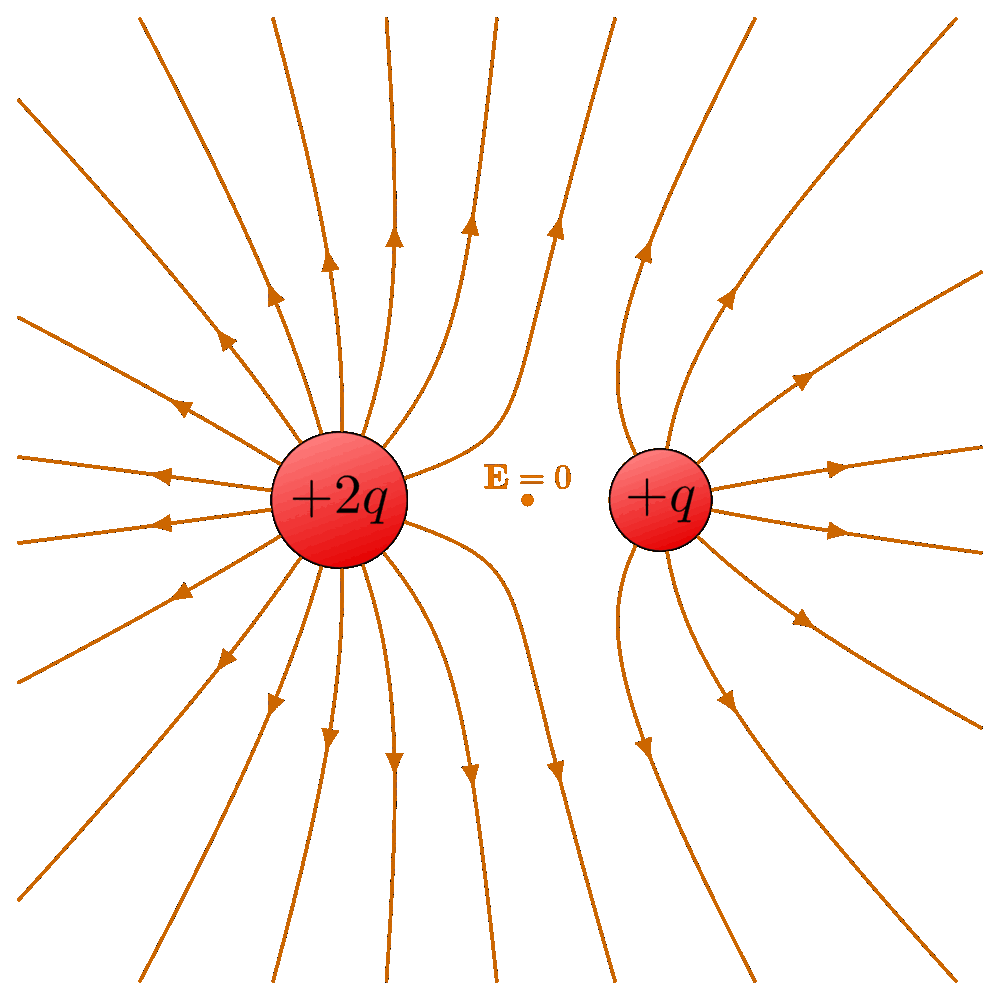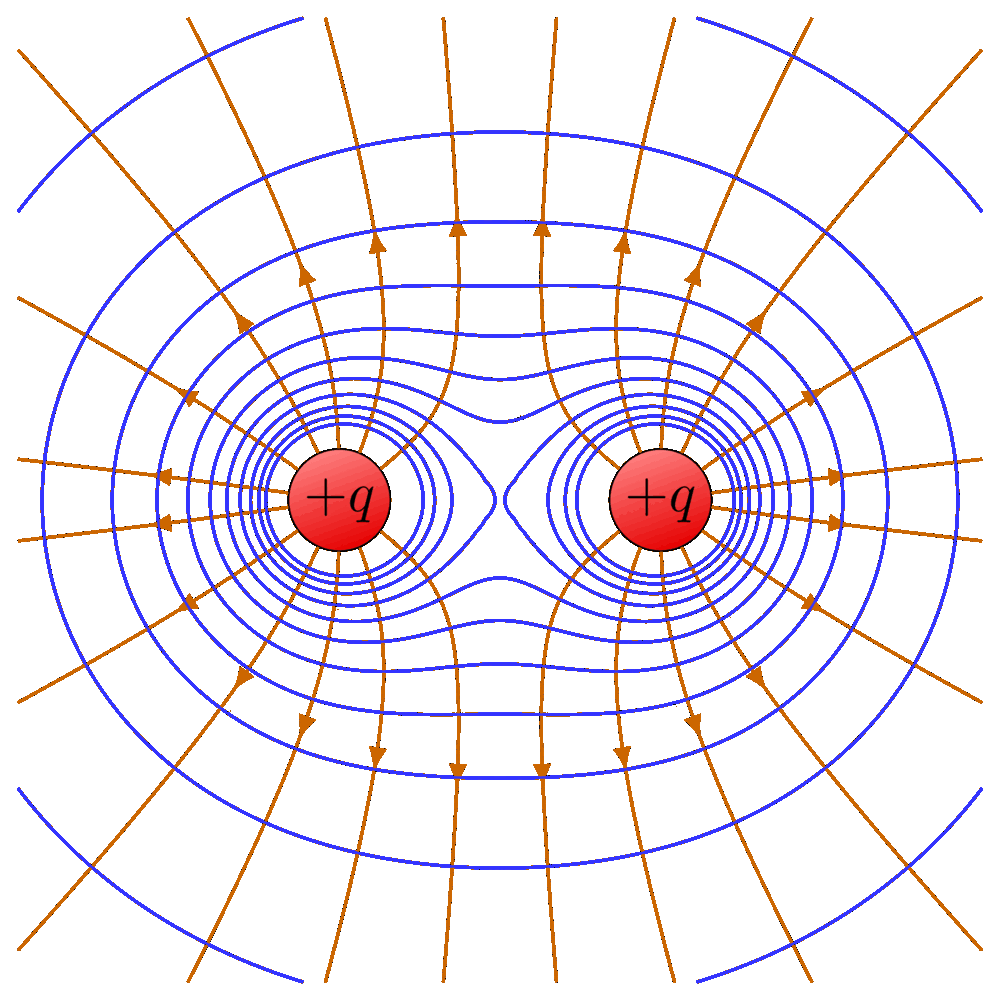
相应地,第二个方程就好理解了。左边的量从电场 E 变成了磁感应强度 B,右边则变成了 0。这又是什么意思呢?比如微分形式,说的是 “一个无限小的封闭曲面内,磁通量等于 0”;积分形式则是 “任意封闭曲面内的总磁通量之和为 0”。
之所以会这样,是因为磁场的磁力线永远是闭合的:一个磁体,无论你怎么切割,它总有 N 极和 S 极,磁力线从 N 极出发,必然会回到 S 极。这意味着,任何封闭曲面内 “穿进” 多少磁力线,就会 “穿出” 多少,总和永远是 0。换句话说,自然界中不存在 “单磁体”(比如只有 N 极或只有 S 极的磁体)。虽然科学家们至今还在努力寻找单磁体,但至少目前,这个方程依然成立。想想看,这条 “高斯磁定律” 是高斯在 200 多年前提出的。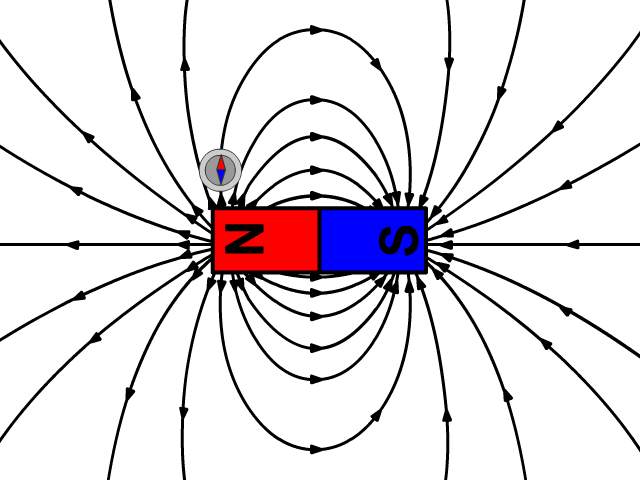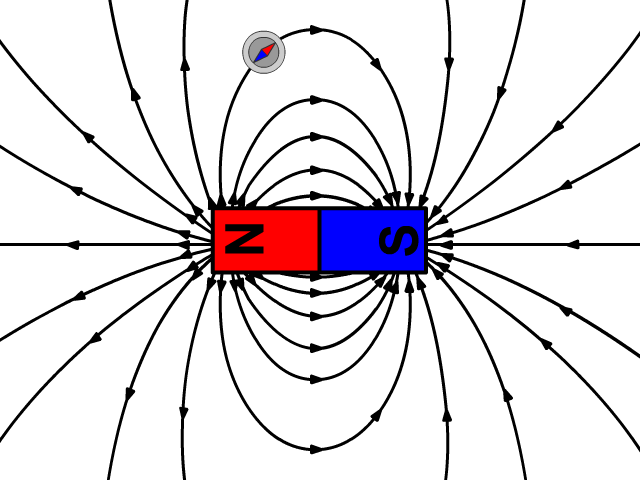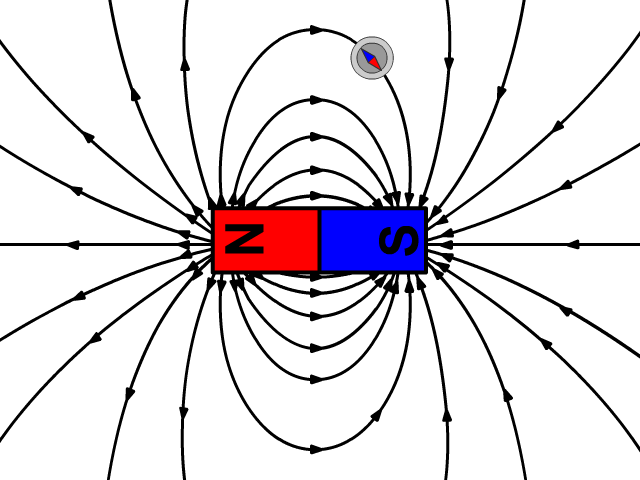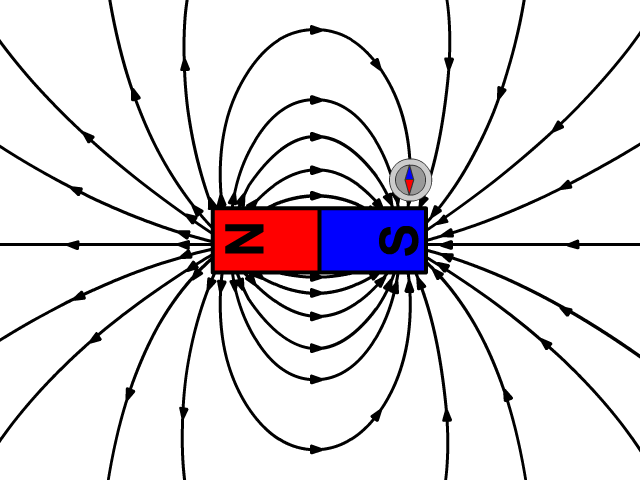
后面两个方程,就更能体现麦克斯韦方程组的“精妙” 了。它们的左边是描述空间特性的量,右边是描述时间变化的量 —— 当 “空间” 和 “时间” 在这里相遇,就产生了奇妙的 “变化”。更有意思的是,方程的一侧是电场 E 或电位移 D,另一侧是磁感应强度 B 或磁场强度 H(注意,E、D、B、H 都是矢量,头顶上都该带箭头)。也就是说,通过 “变化”,电场和磁场被紧紧联系在了一起。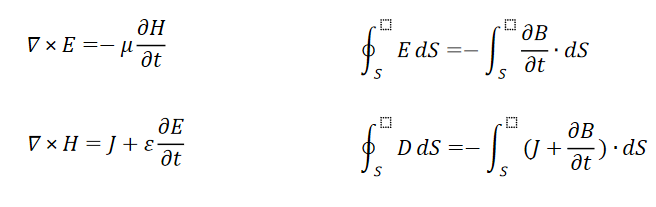
先看第三个方程:随时间变化的磁场,能产生电场。这是法拉第经过无数次实验得出的结论,也是电动机的原理—— 正因为 “变化的磁场生电场”,人类才从蒸汽时代迈入了电力时代。不过要注意,这里的感应电场和电荷产生的电场不一样:电荷产生的电场是 “发散的”,而感应电场是 “漩涡状” 的,就像水流中的漩涡,所以也叫 “漩涡场”。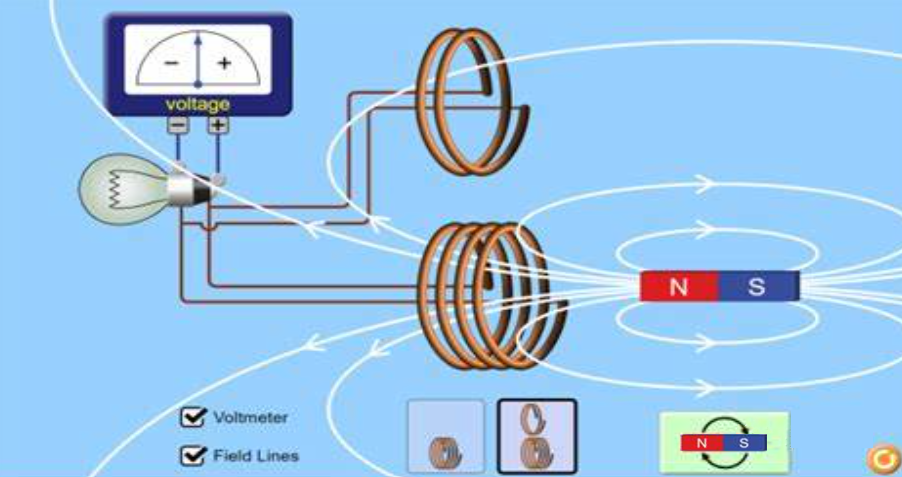
第四个方程,则是麦克斯韦方程组的“点睛之笔”。它告诉我们:不仅电流 J 能产生磁场,变化的电场也能产生磁场。正是这一点,让电和磁实现了 “历史性握手”:变化的电场生磁场,变化的磁场又生电场,如此交替往复,就形成了向前传播的电磁波。我们今天的无线电通信、手机信号、卫星传输,都是靠这种 “交替并进” 的电磁波传递信息的。可以说,正是这两个方程,让 “电” 和 “磁” 不再是孤立的现象,而是统一成了 “电磁场”,为无线时代埋下了伏笔。
讲到这里,或许你对麦克斯韦方程组已经有了些感觉。这时候再回头看那些奇怪的数学符号,可能就没那么“可怕” 了。那个倒三角▽,名叫 “哈密顿算子”,读作 “那勃乐”,它代表着对 x、y、z 三维坐标系的微分运算,而且在运算中既保留了微分的特性,又带着矢量的 “方向感”,就像一把 “矢量手术刀”,能精准 “切割” 空间中的场分布。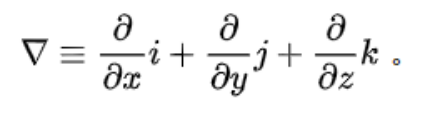
运算方式:
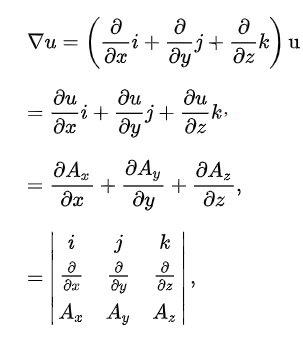
向量点乘:(内积)
点乘(Dot Product)的结果是点积,又称数量积或标量积(Scalar Product)。从代数角度看,点积是对两个向量对应位置上的值相乘再相加的操作,其结果即为点积。从几何角度看,点积是两个向量的长度与它们夹角余弦的积。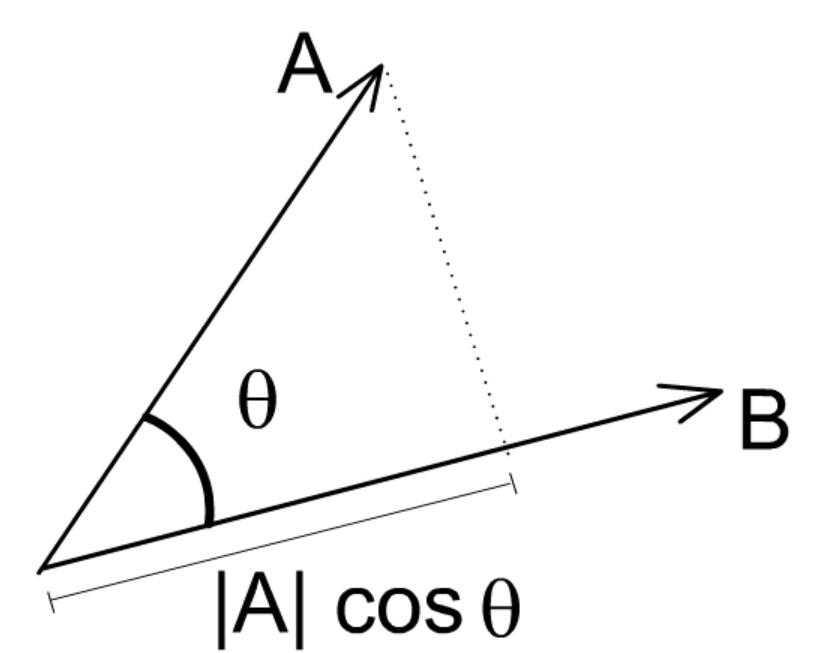
具体来说,▽?描述的是散度,它描述的是矢量场“发散” 的强弱。从物理意义上看,它表示矢量场的 “有源性”:如果散度大于 0,说明这个矢量场在这一点有 “正源”(比如正电荷周围的电场,像泉水一样向外发散);如果散度小于 0,说明有 “负源”(比如负电荷周围的电场,像下水道一样向内汇聚);如果散度等于 0,就说明这里没有 “源”(比如磁场的散度永远为 0,因为没有单磁体)。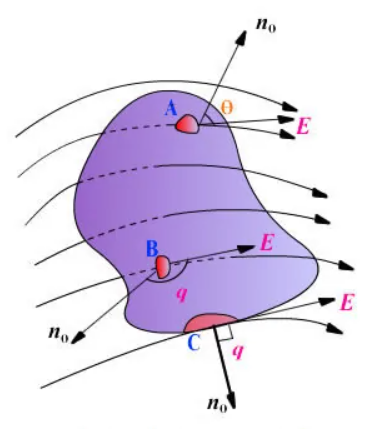
向量叉乘:(外积)
叉乘(Cross Product)又称向量积(Vector Product)。对于三维空间中的两个向量,叉乘的结果是一个新向量 a×b。模长(大小):叉乘结果向量的模长等于两个原始向量的模长与它们夹角的正弦值的乘积。这个模长具有明确的几何意义:它表示以a 和b 为邻边构成的 平行四边形的面积 。因此叉乘的模长反映了两个向量的“垂直程度”。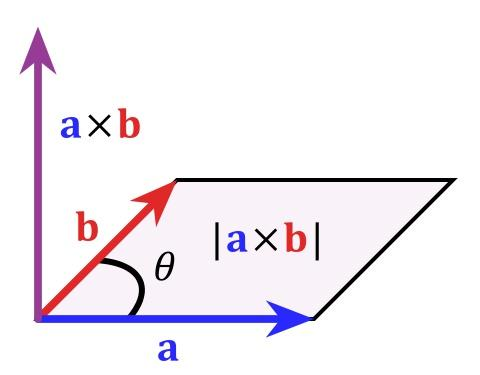
▽× 描述的是旋度,描述的是矢量场在某一点附近的“旋转程度”。旋度矢量的大小,等于 “绕着某一旋转轴的环量” 与 “旋转路径围成的面积” 之比;方向则是这个旋转最剧烈的轴的方向,和旋转方向满足 “右手定则”(比如用右手四指弯曲指向旋转方向,大拇指就是旋度的方向)。比如水流中的漩涡,旋转越急,旋度就越大;而均匀流动的水流,旋度则为 0。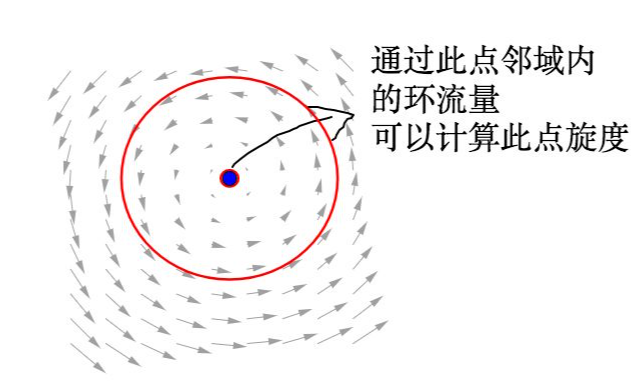
理解了这些符号,再看麦克斯韦方程组,是不是就清晰多了?这组方程看似复杂,却用最简洁的数学语言,揭开了电与磁的神秘面纱,也为射频技术铺就了起点。
审核编辑 黄宇
-
射频
+关注
关注
106文章
5791浏览量
171061 -
麦克斯韦方程组
+关注
关注
0文章
15浏览量
9789
发布评论请先 登录
麦克斯韦方程组究竟带来了什么
麦克斯韦Maxwell方程组是怎么来的
电与磁的开始麦克斯韦方程组到追逐电磁波
电磁场理论之麦克斯韦方程组论文的详细资料免费下载
追逐麦克斯韦方程组与电磁波理论
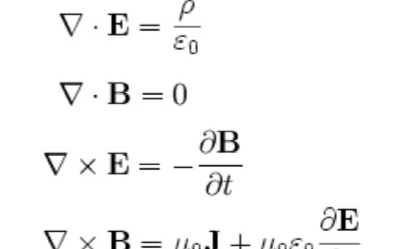
麦克斯韦方程组的详细资料说明

电磁波究竟是如何传播的?一文带你搞懂麦克斯韦方程组
电磁波的传播原理和麦克斯韦方程组的详细说明
射频微波设计入门——麦克斯韦方程组
描述电磁场的麦克斯韦方程组
聊聊介电常数那些事





 射频的起点:从麦克斯韦方程组说起
射频的起点:从麦克斯韦方程组说起

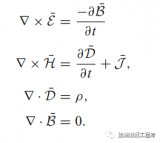










评论