CORDIC算法简介
在信号处理领域,CORDIC(Coordinate Rotation Digital Computer,坐标旋转数字计算机)算法具有重大工程意义。CORDIC算法由Vloder于1959年在设计美国航空导航控制系统时提出,主要用于解决导航系统中三角函数、反三角函数和开方等运算的实时计算问题。
1971年,Walther将圆周系统、线性系统和双曲线系统统一到一个CORDIC迭代方程里,从而额提出了一种统一的CORDIC算法形式。
CORDIC算法的核心是利用加法和移位的迭代操作去替代复杂的运算,从而非常有利于硬件实现。CORDIC算法应用广泛,如离散傅里叶变换(DFT)、离散余弦变换(DCT)、离散Hartley变换、Chirp-Z变换、各种滤波以及矩阵中的奇异值分解。
在工程领域,可采用CORDIC算法实现直接数字频率合成器(DDS)、计算I/Q信号的幅度和相位。
01CORDIC基本原理
我们假设在笛卡尔坐标系(也就是我们常见的XY直角坐标系)中,将点(x1,y1)旋转θ角度到点(x2,y2)的标准方法如下所示:
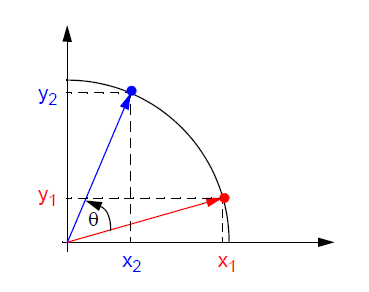
根据上图,我们利用高中学习的三角函数、圆方程和极坐标等中学知识,可以得到:
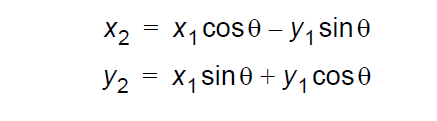
这被称为是平面旋转、向量旋转或者线性 ( 矩阵) 代数中的 Givens 旋转。
上面的式子,我们将大学二年级学习的线性代数知识拿出来,用矩阵的形式来表示,于是得到:
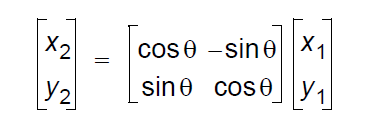
例如,我们做一个90°的相移,即θ=90:
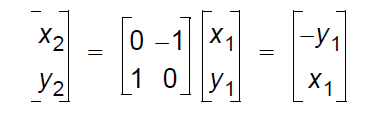
这里注意cos和sin函数在直角坐标系下的物理意义,于是我们得到下面的图示。
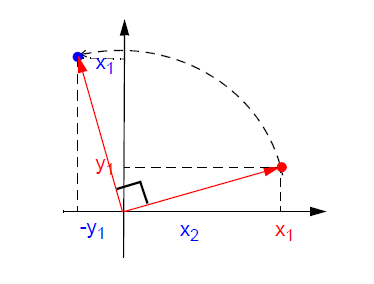
上面的第一个式子,我们假设提出一个公因子cosθ,那么我们可以得到:
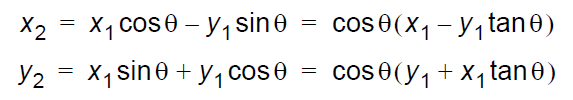
如果去除项,我们得到 伪旋转 方程式 :
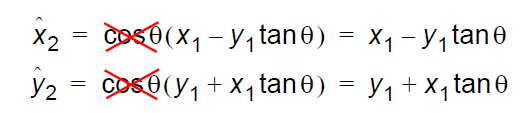
即旋转的角度是正确的,但是x 与 y 的值增加cos-1θ 倍 ( 由于cos-1θ》 1),所以模值变大。
注意我们并不能通过适当的数学方法去除cosθ 项 , 然而随后我们发现去除项可以简化坐标平面旋转的计算操作。
怎么说呢?
在XY坐标系中,结合上面的伪旋转公式,我们可以用下图表示:
于是,我们得出以下结论:
经过伪旋转之后,向量 R 的模值将增加1/cosθ 倍。
向量旋转了正确的角度 , 但模值出现错误。
经过伪旋转后, 输出进行适当的幅度伸缩(1/cosθ),是不是就可以得到旋转后的坐标了。
02CORDIC方法
CORDIC 方法的核心是 ( 伪) 旋转角θ,其中,
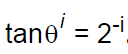
这个等式是怎么推导出来的呢?
所以方程为:
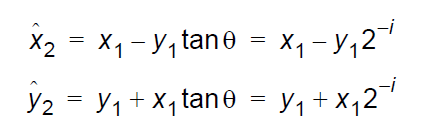
下面的表格指出用于 CORDIC 算法中每个迭代 (i) 的旋转角度 (精确到 9位小数):
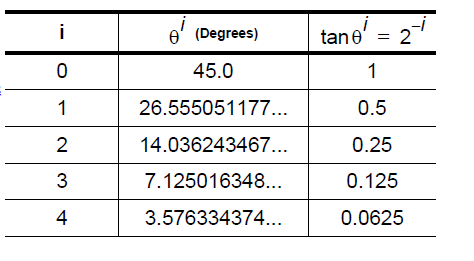
note:由于i是整数,所以对应的角度值都是一一确定的,只能通过几个角度的加减组合来达到你所想要的角度值。
注意有三个方面的变化:
角度累加(减)
坐标值累加(减)
向量的模(也就是长度的,相对于横纵坐标的)累加(减)
这三个累加的变化时不一样的,注意区别,角度的累加和长度的累加有一定的对应关系。
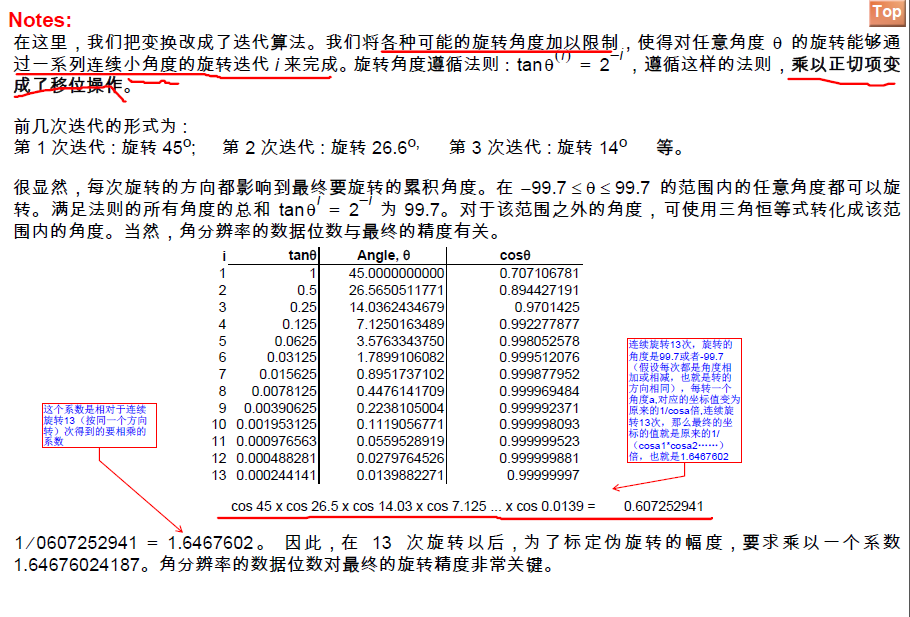
03角度累加器


上述三个方程式为圆周坐标系中用于角度旋转的 CORDIC 算法的表达式。后续部分中我们还将看到CORDIC 算法被用于其它的坐标系,通过使用这些坐标系可以执行更大范围的函数计算。
04移位-加法算法
因此, 原始的算法现在已经被减化为使用向量的伪旋转来表示的迭代移位-相加算法 :
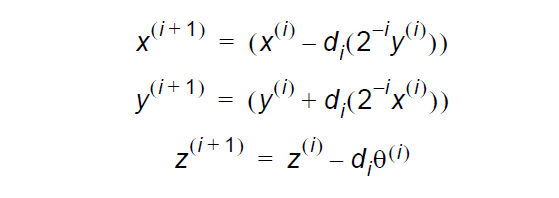
因此,每个迭代需要:

note:前面提到的去除 cos 项的原因是显而易见的。当将该项去除时,转换公式已经被简化为伪旋转的迭代移位相加计算。
CORDIC 硬件实现结构:
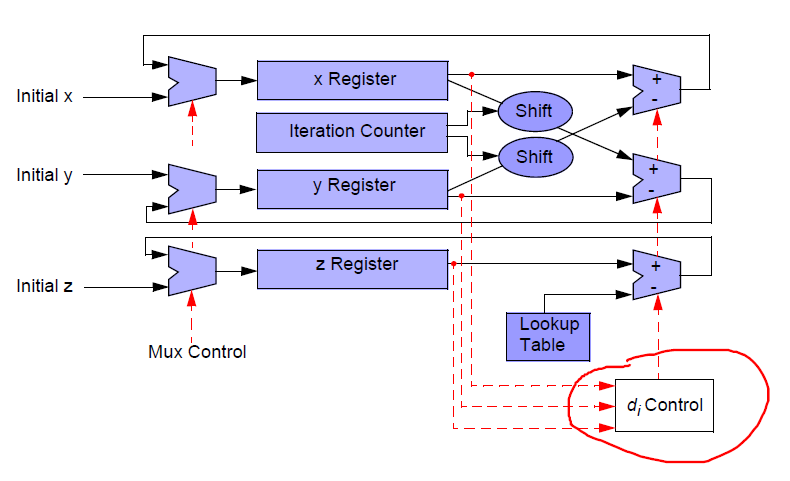
05伸缩因子
前面提到,为了得到伪旋转公式,我们把公因子cosθ忽略了,但在实际运算中,不能就这样简单粗暴抛弃。
我们再次对cosθ进行变形:

于是,我们可以得到:

如果我们已知了将被执行的迭代次数,我们便可以预先计算出 1/Kn 的值,并通过将 1/Kn 与 x(n) 和 y(n)相乘来校正x(n) 和 y(n) 的最终值。
CORDIC有两种工作模式:旋转模式和向量模式。

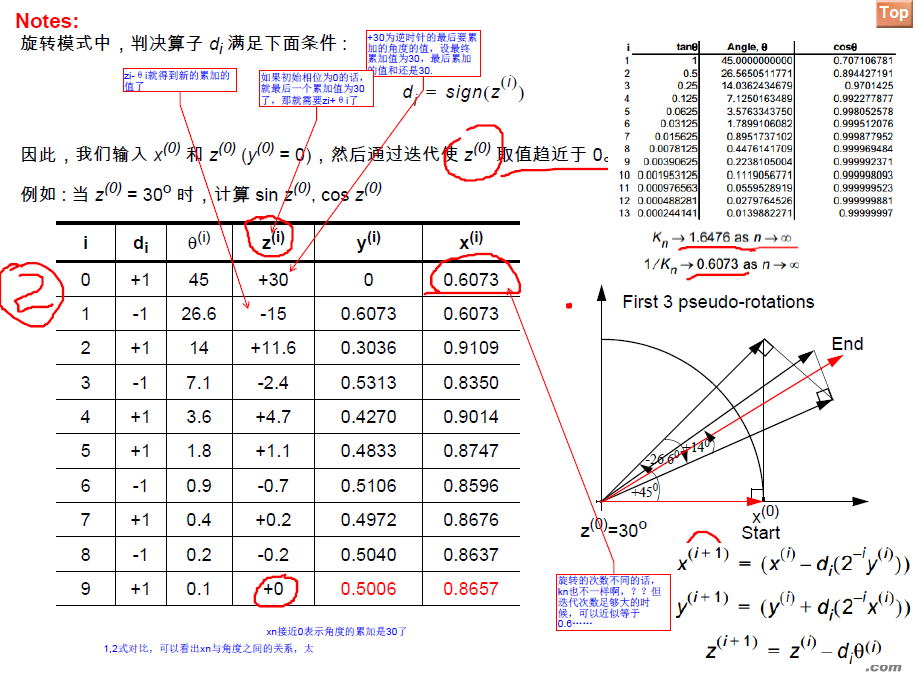

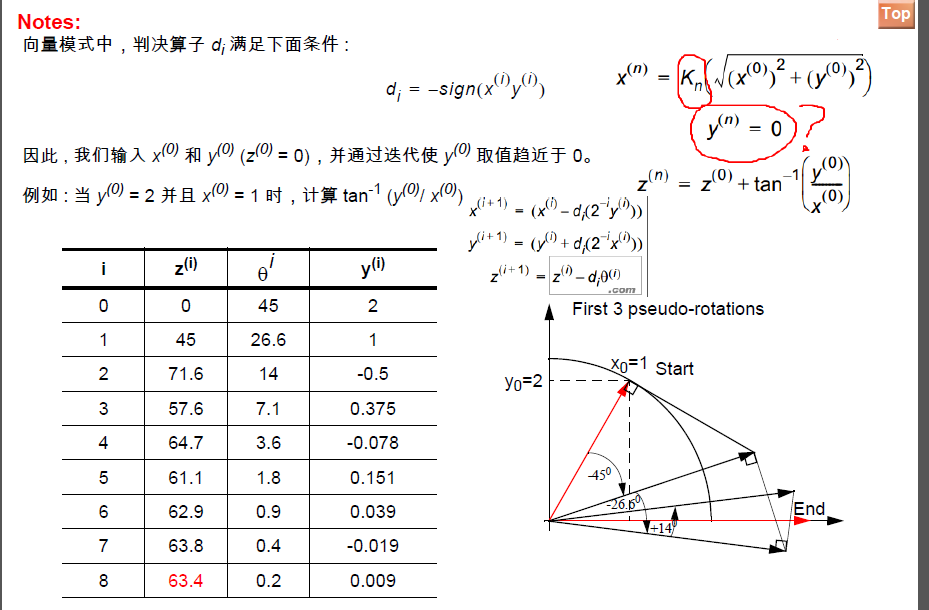
06三种坐标系下的CORDIC
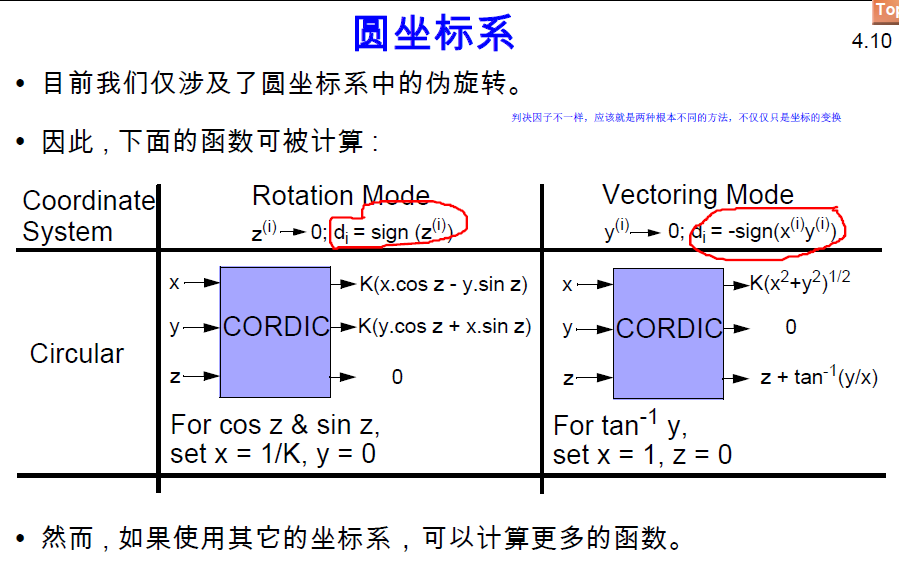
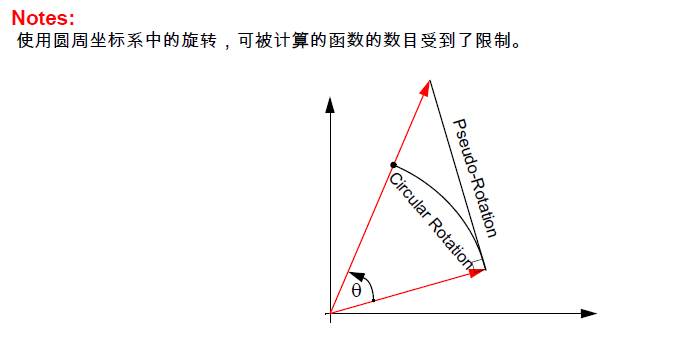
然而, 我们将会看到,通过考虑其它坐标系中的旋转, 我们可以直接计算更多的函数, 如乘法和除法, 进而间接计算更多的其它函数。
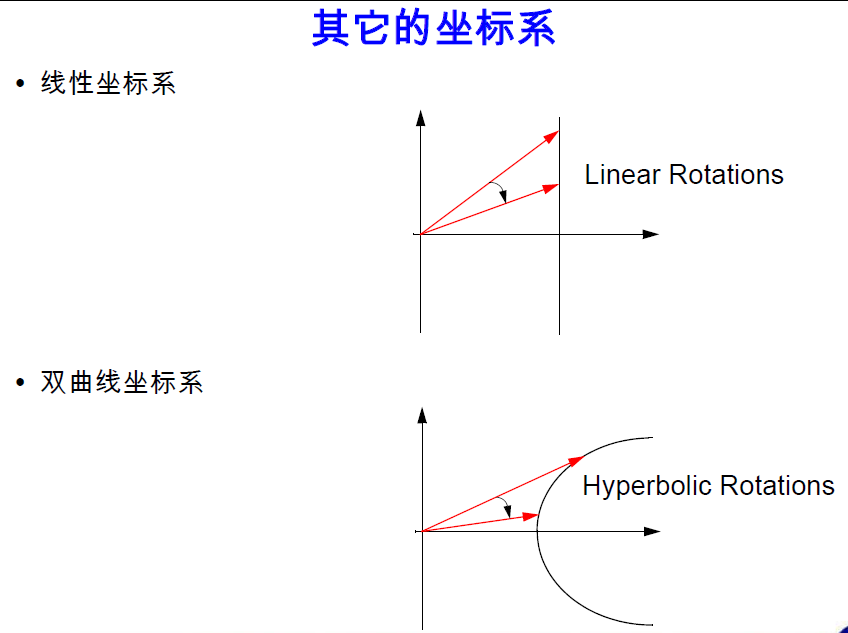
使用其它坐标系的 CORDIC 算法的优点是可以计算更多的函数, 而缺点则是系统将变得更加复杂。当把CORDIC 算法用于线性或双曲坐标系时, 在圆周坐标系中的旋转角度集将不再有效。所以, 这些系统应使用其它的两种旋转角度集。
我们会发现,可以推导出可在 3 个坐标系中表示 CORDIC 方程的通用公式。这意味着在方程式中引入两个新变量。其中一个新变量 (e(i)) 代表了适当的坐标系中用于表示旋转的角度集。
当把CORDIC算法用于双曲线旋转时,伸缩因子K与圆周旋转的因子有所不同。

我们通过引入一个新变量μ,得到CORDIC的通用方程:

至此,三个坐标系下的CORDIC方程得到大一统。



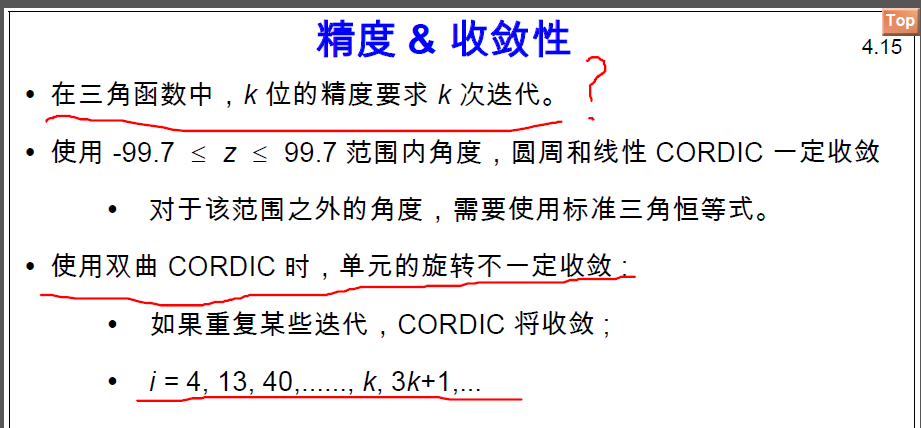
在使用FPGA进行CORDIC算法实现时,理想CORDIC 架构取决于具体应用中速率与面积的权衡。
可以将 CORDIC 方程直接翻译成迭代型的位并行设计,然而:
位并行变量移位器不能很好地映射到 FPGA 中
需要若干个 FPGA 单元。导致设计规模变大而设计时间变长
参考文献
关于 CORDIC 算法的基础以及细节问题,可参见下面的材料 :
[1] R. Andraka. A survey of CORDIC algorithms for FPGA based computers. www.andraka.com/cordic.htm
[2] The CORDIC Algorithms. www.ee.byu.edu/ee/class/ee621/Lectures/L22.PDF
[3] CORDIC Tutorial. http://my.execpc.com/~geezer/embed/cordic.htm
[4] M. J. Irwin. Computer Arithmetic. http://www.cse.psu.edu/~cg575/lectures/cse575-cordic.pdf
编辑:jq
-
计算机
+关注
关注
19文章
7679浏览量
91005 -
COS
+关注
关注
1文章
24浏览量
20267 -
CORDIC算法
+关注
关注
0文章
17浏览量
9874
原文标题:什么是CORDIC算法
文章出处:【微信号:HXSLH1010101010,微信公众号:FPGA技术江湖】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
一文带你了解什么是机器视觉网卡

一文带你了解电源测试系统的功能!

一文了解电压谐波

【微五科技CF5010RBT60开发板试用体验】Cordic数学计算测试
带你一文了解芯片开封技术

一文带你了解arm主板

一文带你了解FIB技术
一文带你了解工业电脑

一文带你了解什么是SD NAND存储芯片
一文带你了解透过率测量
一文带你了解IP地址别名
一文带你了解IP版本

一文带你了解半导体公司的各个岗位






 一文带你们了解什么是CORDIC算法
一文带你们了解什么是CORDIC算法












评论